How to make interactive plots based on MPQr distances

Introduction

In this vignette, we will show how to use the MPQ distance family to investigate patterns of beta diversity. To illustrate the tool, we will analyze the dataset collected by Alwyn Gentry way back when. Our analysis here is based on a version of the dataset that David Zeleny posted on his anadat-r repository. A phylogeny was built from the taxonomic information using S.PhyloMaker, and higher-order taxonomic information was inferred using taxonlookup. We did a good deal of data cleaning, and all of the choices we made can be seen in the script at data-raw/gentry.R in this package.

Seting up and transformations

We start off by loading the packages we need for this analysis and loading the gentry data, our version of which is available as a phyloseq object. This object includes the counts of each species observed at each of the sites, phylogenetic and taxonomic information about the species, and information (latitude, longitude, elevation, and precipitation) about each of the sites.

library(ape)
library(mpqDist)
library(plotly)
library(phyloseq)
library(tidyverse)
library(viridis)
library(plotly)
library(fields)
library(compositions)
data(gentry)
gentry
#> phyloseq-class experiment-level object
#> otu_table()   OTU Table:         [ 585 taxa and 197 samples ]
#> sample_data() Sample Data:       [ 197 samples by 4 sample variables ]
#> tax_table()   Taxonomy Table:    [ 585 taxa by 4 taxonomic ranks ]
#> phy_tree()    Phylogenetic Tree: [ 585 tips and 349 internal nodes ]

Here we will apply a started log transform to the counts. We will show the same analysis below with the raw data or relative abundance data, but we believe the log transformation is generally beneficial. This is discussed in more detail in the paper, but there are two primary reasons for this. First, ratios tend to be more comparable than differences for abundance data. Second, the counts tend to have a very skewed distribution, which results in distances involving sites with very high abundances of a specific species to be very large.

The patterns tend to be the same with the log-transformed vs. raw data, but the values are more stable and the resulting patterns are easier to see with the log transformation.

Here we apply a started log transform to the abundances and we show the distributions of the raw and log-transformed abundances. The transformed abundances are still skewed, but to a lesser extent than the raw abundances. The plot below shows the distribution of non-zero abundances. The fraction of abundances that are 0 is about 99%.

mean(otu_table(gentry) == 0)
#> [1] 0.990325
gentry_log = gentry
otu_table(gentry_log) = otu_table(clr(1 + otu_table(gentry)), taxa_are_rows = FALSE)
abundance_df = data.frame(abundances = c(otu_table(gentry), otu_table(gentry_log)),
                          type = rep(c("raw", "transformed"), each = ntaxa(gentry) * nsamples(gentry)))
ggplot(subset(abundance_df, abundances > 0)) + geom_histogram(aes(x = abundances), bins = 100) +
    facet_wrap(~ type, scales = "free_x")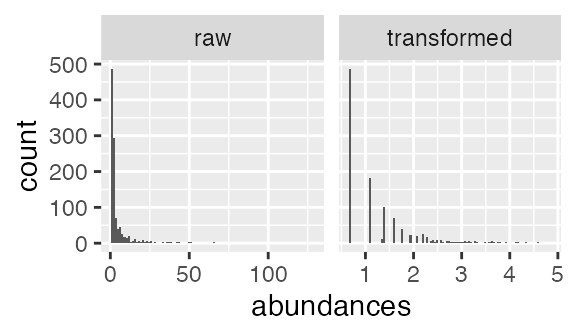

Distributions of raw and transformed abundances

Computing the distances

The get_mpq_distances function will compute the full range of MPQr distances, with r taking values between 0 and 1. r = 0 corresponds to the standard Euclidean distance, small values of r can be interpreted as measuring “terminal” phylogenetic dissimilarity, and large values of r can be interpreted as measuring “basal” phylogenetic dissimilarity. Its first argument should be a matrix (or something that inherits from a matrix, like the otu_table object below). Its second argument should be a phylogenetic tree of class phylo. You can specify a set of values of r to compute if you would like. If you don’t specify anything, the default is to take a range of 101 values between 0 and 1 such that the are spaced more closely near 0 and 1 and farther apart in the middle. There is not a good theoretical reason for this, but it has worked well in all the examples we have looked at.

distances = get_mpq_distances(otu_table(gentry_log), phy_tree(gentry_log))

Built-in functions for interactive plots

It is easiest to visualize the family of distances with an animated plot. This package includes some helper functions that allow the user to make a couple of different kinds of plots and gives templates so as to allow the user to make custom versions if the ones included here are not suitable.

Plot distance to a reference set

The first kind of plot supported is one that shows the distance of each individual sample to a set of “reference” samples. This sort of plot would be of use if, for example, you had samples collected from sites along a river and you wanted to visualize the distance between each site and a reference site at one end of the river. The function that computes this is called plot_dist_to_reference_samples.

The required arguments are

• physeq: A phyloseq object containing the species abundances at each site, a phylogenetic tree describing the species, and a sample data matrix with information about the sites.
• reference_samples: A vector containing either the names or the indices of the reference sites.
• x_variable: A string giving the name of the variable to plot on the x-axis.

As an example, the code below gives us a plot where each point corresponds to a site, its position on the y-axis corresponds to the average distance between that site and the sites near the equator, and its position on the x-axis corresponds to its latitude.

equatorial_samples = sample_names(gentry_log)[which(sample_data(gentry_log)$Lat >= -10 & sample_data(gentry_log)$Lat <= 10)]
plot_dist_to_reference_samples(physeq = gentry_log, reference_samples = equatorial_samples,
                               x_variable = "Lat")

The function also allows for extra aesthetics to be passed to ggplot when it is building the plot. For example, if you want to have the points colored by Elevation, you would specify color = "Elevation" in plot_dist_to_reference_samples. The plot is built using aes_string in ggplot, so any aesthetics that geom_point understands can be specified in this way.

plot_dist_to_reference_samples(physeq = gentry_log, reference_samples = equatorial_samples,
                               x_variable = "Lat", color = "Elev", size = "Precip")

Finally, if you want to be able to customize the plot more fully, there is an option for the function to return a ggplot object which can then be turned into an animated plot by calling the ggplotly function on that object. The advantage of this way of doing things is that the ggplot object can be modified before being made into an animated plot, allowing for more customization. For example, if we wanted to change the color scale, reverse the x axis, and add a loess smoother, we could do it as follows:

p = plot_dist_to_reference_samples(physeq = gentry_log, reference_samples = equatorial_samples,
                                   x_variable = "Lat", color = "Elev", return_ggplot = TRUE) +
    stat_smooth(aes(frame = frame), se = FALSE) + 
    scale_x_reverse() +
    scale_color_viridis()
ggplotly(p)
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'

Plot all pairs of distances

Another kind of plot that can be useful is one where the difference between each pair of sites is plotted. The standard here would be to have one point for each pair of samples, to plot the MPQr distance on the vertical axis and the geographical distance on the horizontal axis.

To make this sort of plot, you can use the function plot_all_pairs. This function takes the following arguments:

• phy: A phyloseq object, the same as plot_dist_to_reference_samples.
• sample_distances: Either a matrix or an object of class dist containing the geographic distances between the samples. plot_all_pairs assumes that the samples in these objects are in the same order as the samples in phy.
• return_ggplot: Optional argument to return a ggplot object instead of plotting with ggplotly. By default return_ggplot is FALSE.

Since the number of pairs of distances grows with the square of the number of sites, it takes a long time to compute all pairs of distances in this dataset. I will therefore restrict just to the sites in Eastern North America. The code block below shows the locations of all the sites in the dataset and has the Eastern North American subset marked.

sample_data(gentry_log)$ena_subset = sample_data(gentry_log)$Lat > 25 & sample_data(gentry_log)$Long < 0 & sample_data(gentry_log)$Lat < 50
ggplot(sample_data(gentry_log)) +
    borders("world", colour = "gray70", fill = "gray90") +
    geom_point(aes(x = Long, y = Lat, shape = ena_subset, color = Elev)) + coord_fixed(1.3)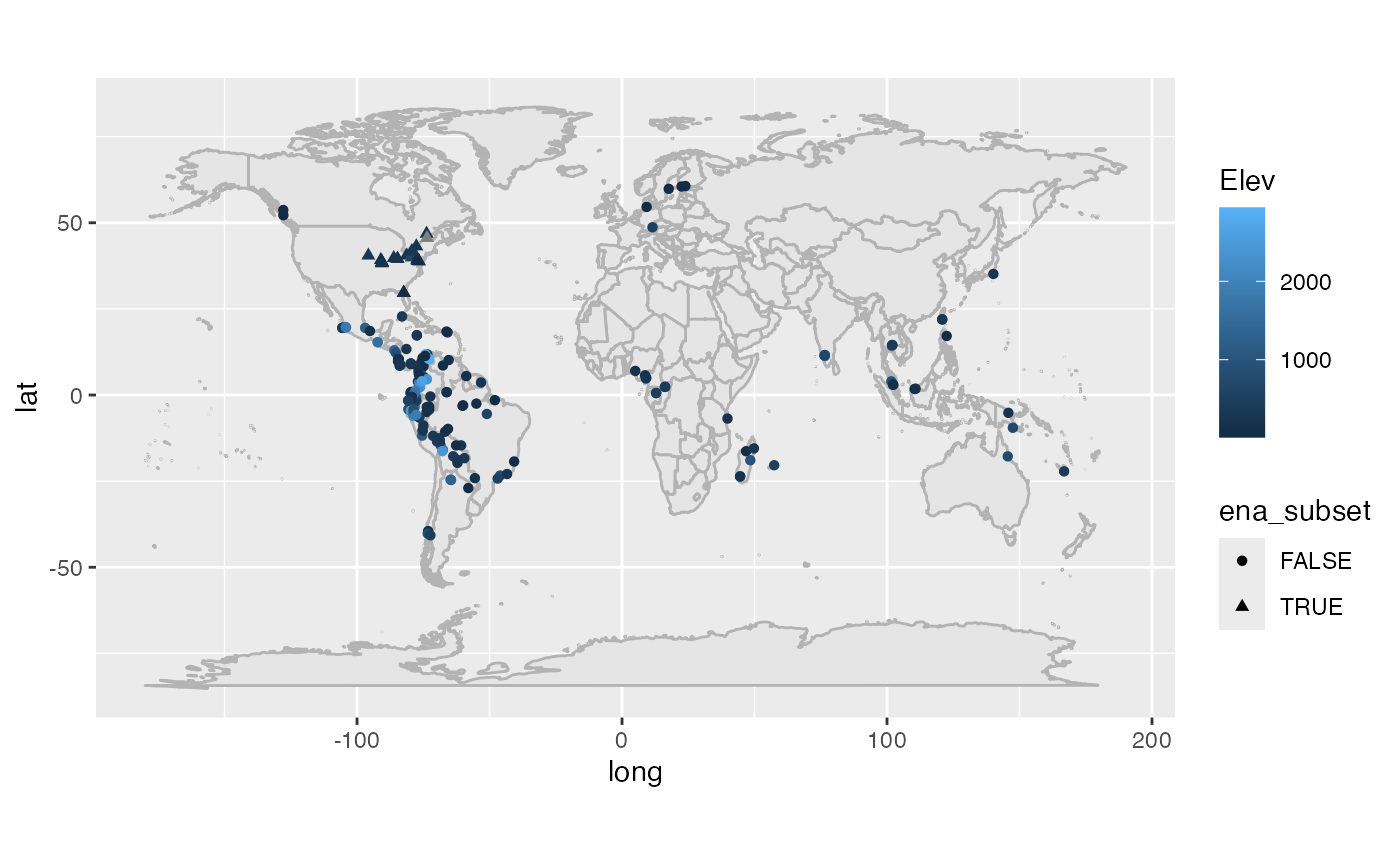

gentry_log_ena_subset = subset_samples(gentry_log, ena_subset)

Next, we compute the distances between the sites (in this case, using rdist.earth, which computes great circle distances), and use those distances as input to plot_all_pairs. In this case, plot_all_pairs was called with return_ggplot = TRUE, which returns a ggplot object and allows me to add a smoother. Finally, calling ggplotly(p) creates the interactive plot.

greatcircle_sample_distances = rdist.earth(as.matrix(sample_data(gentry_log_ena_subset)[,c("Long", "Lat")]))
p = plot_all_pairs(gentry_log_ena_subset, greatcircle_sample_distances, return_ggplot = TRUE)
p = p + stat_smooth(aes(frame = frame), se = FALSE)
ggplotly(p)
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'

Helper functions for custom interactive plots

The package also includes helper functions that allow for more customization, but since the interactive plots are based on ggplotly, some knowledge of how ggplotly works is necessary to use these functions. Briefly, to convert a standard ggplot2 plot to an animated plot with ggplotly, you modify the plotting data frame so that it has an extra column that specifies the “frame” of the animation, add that as part of the aesthetic mapping (e.g. aes(frame = frame)) in the ggplot, and then call the ggplotly function on the resulting ggplot object. For more details, see the ggplotly documentation on animations.

The make_animation_df function

The make_animation_df can help make this sort of data frame. Its first argument is the output of get_mpq_distances (a list with elements distances and r), and its second argument is a function that takes a single distance object and returns a data frame with the variables needed to make one frame of the animation. Extra arguments can be passed to the function that makes the data frame if necessary. This function will be applied to each of the elements of the distances slot of the output of get_mpq_distances, the resulting data frames will be bound together, and a column will be added indicating the frame of the animation (one frame per value of r).

Once this data frame has been created, the user can make an animated plot by adding frame = frame to the aesthetic specification of the ggplot they would use for a static plot. Calling ggplotly on the resulting ggplot object will make an animated plot.

Function to create plotting variables

In the code block below, we show an example of creating the data frame that we need to make an interactive plot. The make_animation_df function in the last line of that block takes as its first argument mpq_distances (the output from the get_mpq_distances function). Its second argument is a function, get_avg_distances_to_set. The get_avg_distances_to_set function in turn has three arguments, which are given as the final three arguments to make_animation_df and which that function passes along to get_avg_distances_to_set. So in this case, inside the make_animation_df function, there is a call to get_avg_distances_to_set(nmv, equatorial_samples, sample_data(gentry_log)).

equatorial_samples = sample_names(gentry_log)[which(sample_data(gentry_log)$Lat >= -10 & sample_data(gentry_log)$Lat <= 10)]
nmv = get_null_mean_and_variance(gentry_log)
mpq_distances = get_mpq_distances(otu_table(gentry_log), phy_tree(gentry_log))
animation_df = make_animation_df(mpq_distances, get_avg_distances_to_set, means_and_vars = nmv, equatorial_samples, sample_data(gentry_log))

Finally, once we have the animation_df data frame, we can make an animated plot. We start off making p, a ggplot object, that specifies the sort of plot we want for each value of r. In each aes specification, we add frame = frame, which will make the plot scroll through the different values of r. Finally we call ggplotly on p to make the interactive plot.

p = ggplot(aes(x = Lat, y = avg_dist, color = Elev), data = animation_df) +
    geom_point(aes(frame = frame)) +
    geom_hline(aes(yintercept = null_mean, frame = frame)) +
    geom_hline(aes(yintercept = null_mean - 2 * null_sd, frame = frame)) +
    geom_hline(aes(yintercept = null_mean + 2 * null_sd, frame = frame)) +
    stat_smooth(aes(frame = frame), se = FALSE, method = "gam") +
    scale_x_reverse() +
    scale_color_viridis()
ggplotly(p)
#> `geom_smooth()` using formula = 'y ~ s(x, bs = "cs")'

Code to create plots in manuscript

The following code makes a plot that is in the manuscript, comparing MPQr distances to each other, to Bray-Curtis, and to distances computed on agglomerated species counts.

mpq_distances = get_mpq_distances(otu_table(gentry_log), phy_tree(gentry_log))

## compute Bray-Curtis dissimilarity on untransformed data
mpq_distances$distances[["bray"]] =  distance(gentry, method = "bray")
mpq_distances$r = c(mpq_distances$r, "bray")
## agglomerate the untransformed data to order level, then clr-transform the agglomerated data
gentry_order_glom = tax_glom(gentry, taxrank = "order")
gentry_log_order_glom = gentry_order_glom
otu_table(gentry_log_order_glom) = otu_table(clr(otu_table(gentry_order_glom) + 1), taxa_are_rows = FALSE)
## agglomerate the untransformed data to order level, then clr-transform the agglomerated data
gentry_group_glom = tax_glom(gentry, taxrank = "group")
gentry_log_group_glom = gentry_group_glom
otu_table(gentry_log_group_glom) = otu_table(clr(otu_table(gentry_group_glom) + 1), taxa_are_rows = FALSE)

## compute Euclidean distances on the clr-transformed agglomerated data
mpq_distances$distances[["order_glom"]] = dist(otu_table(gentry_log_order_glom))
mpq_distances$r = c(mpq_distances$r, "order_glom")
mpq_distances$distances[["group_glom"]] = dist(otu_table(gentry_log_group_glom))
mpq_distances$r = c(mpq_distances$r, "group_glom")

## we will compare to the northern temperate samples
temperate_samples = sample_names(gentry_log)[which(sample_data(gentry_log)$Lat >= 23.5 & sample_data(gentry_log)$Lat <= 66.5)]


## this is a roundabout way of doing things, but make_animation_df
## here sets up the data for plotting for the MPQr distances + Bray
## Curtis + Euclidean distance on agglomerated data. I will use a subset of it to plot later
animation_df = make_animation_df(mpq_distances, get_avg_distances_to_set, means_and_vars = NULL, temperate_samples, sample_data(gentry_log))

## I will be plotting mpqr distances with r = 0, 1, .7 + bray-curtis + Euclidean distance on two levels of agglomeration
mid_r = "0.712889645782536"
animation_df_sub = subset(animation_df, frame %in% c(mid_r, "0", "1", "bray", "order_glom", "group_glom"))
## this data frame will allow me to plot averages in 15-degree-of-latitude bins
animation_df_summarised = animation_df_sub |>
    mutate(latitude_bin = round(Lat / 15) * 15) |>
    group_by(frame, latitude_bin) |> summarise(mean_in_bin = mean(avg_dist), se_in_bin = sd(avg_dist) / sqrt(length(avg_dist)))
#> `summarise()` has grouped output by 'frame'. You can override using the
#> `.groups` argument.
## making frame into an ordered factor so that the facots are plotted in the order I want
animation_df_sub$frame = factor(animation_df_sub$frame,
                                levels = c("0", mid_r, "1", "bray", "order_glom", "group_glom"),
                                ordered = TRUE)
animation_df_summarised$frame = factor(animation_df_summarised$frame,
                                       levels = c("0", mid_r, "1", "bray", "order_glom", "group_glom"),
                                       ordered = TRUE)

## to do custom facet labels
frame_labels <- c("0" = "r = 0",
                  mid_r = paste("r = ", round(as.numeric(mid_r), digits = 2), sep = ""),
                  "1" = "r = 1",
                  "bray" = "Bray-Curtis",
                  "order_glom" = "Glommed to order",
                  "group_glom" = "Glommed to phylum")
names(frame_labels)[2] = mid_r
#pdf("gentry-latitudinal-distance.pdf", width = 7, height = 5)
ggplot(data = animation_df_sub) +
    geom_point(aes(x = Lat, y = avg_dist), size = .8, color = 'gray', pch = 1) +
    geom_errorbar(aes(x = latitude_bin,
                      ymin = mean_in_bin - 2 * se_in_bin,
                      ymax = mean_in_bin + 2 * se_in_bin),
                  data = animation_df_summarised,
                  width = 6) +
    annotate("rect",
           xmin = 23.5, xmax = 66.5,   # x-range to shade
           ymin = -Inf, ymax = Inf,  # full y-range
           alpha = 0.2, fill = "blue") + 
    geom_point(aes(x = latitude_bin, y= mean_in_bin),
               data = animation_df_summarised) +
    geom_line(aes(x = latitude_bin, y= mean_in_bin),
               data = animation_df_summarised) +
    scale_x_reverse(breaks = seq(60, -40, by = -20)) +
    xlab("Latitude") + ylab("Average distance to northern temperate sites")+
    facet_wrap( ~ frame, scales = "free_y", ncol = 3,
               labeller = labeller(.default = frame_labels))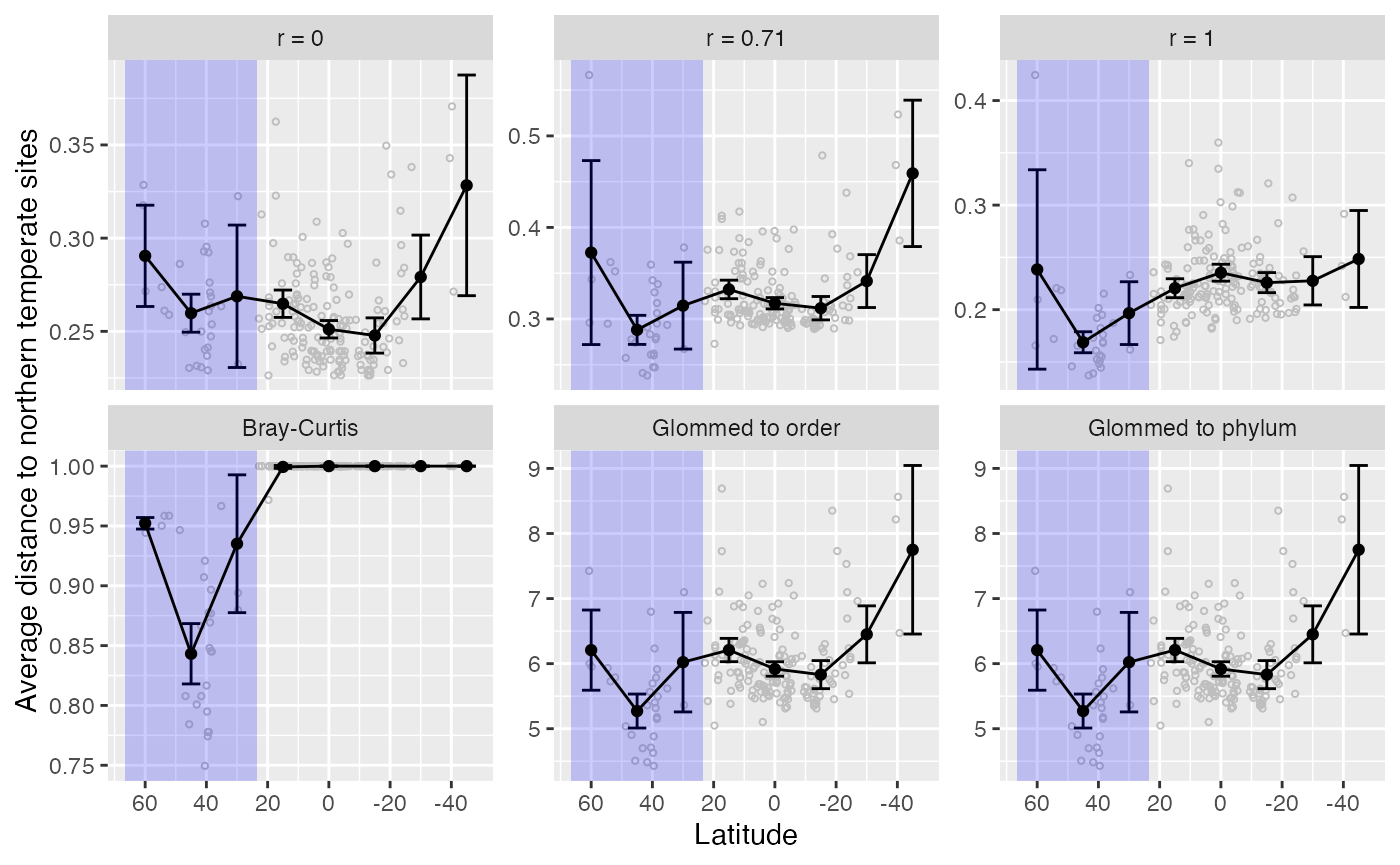

#dev.off()