Descent methods for unconstrained problems

Agenda today

Gradient descent and steepest descent for unconstrained problems
Convergence analysis
Relationship with Newton's method

Reading:

Boyd and Vandenberghe, Chapter 9.1-9.4

The problem we want to solve

\[ \text{minimize}_x \quad f(x) \]

Descent Methods

General algorithm:

Start with a point \(x\)

Repeat

Choose a descent direction \(\Delta x\)
Choose step size \(t\).
Update: \(x \leftarrow x + t \Delta x\)

Until the stopping criterion is satisfied, usually \(\|\nabla f(x)\|_2 \le \epsilon\).

Line search types: Exact line search

Step size \(t\) found as \[ t = \text{argmin}_{t > 0}f(x + t \Delta x) \]

This can be useful if there is an analytic or otherwise quick method of finding the minimum of the function restricted to a ray.

Line search types: Backtracking line search

Step size \(t\) found with an iterative method.
Parameters \(\alpha \in (0, 1/2)\), \(\beta \in (0,1)\) that you specify.
Algorithm: Start at \(t = 1\), repeat \(t \leftarrow \beta t\) until \[ f(x + t \Delta x) < f(x) + \alpha t \nabla f(x)^T \Delta x \]

Gradient descent

In gradient descent, we take \(\Delta x = - \nabla f(x)\).

Overall algorithm:

Start with a point \(x\)

Repeat

\(\Delta x \leftarrow - \nabla f(x)\).
Line search: Choose step size \(t\) by either backtracking line search or exact line search.
Update: \(x \leftarrow x + t \Delta x\)

Until the stopping criterion is satisfied, usually \(\|\nabla f(x)\|_2 \le \epsilon\).

Convergence time for gradient descent

If \(f\) is strongly convex, we have the result \[ f(x^{(k)}) - p^\star \le c^k (f(x^{(0)}) - p^\star) \]

\(c \in (0,1)\) depends on properties of the function and the line search type
Much slower (in terms of iterations) than Newton's method
But: we don't have to compute a Hessian

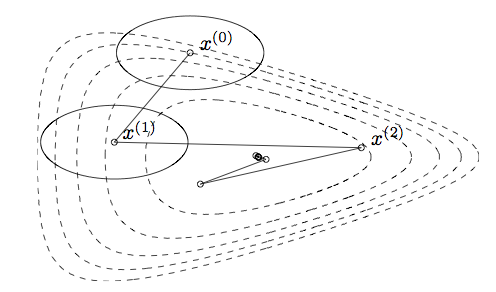
Gradient descent example

Iterates of gradient descent with backtracking line search, for minimizing \(f(x_1, x_2) = \exp(x_1 + 3 x_2 - .1) + \exp(x_1 - 3 x_2 - .1) + \exp(-x_1 - .1)\)

Contours represent the boundaries of the sublevel sets of the function: \(\{x : f(x) \le a\}\).

Steepest descent

Steepest descent: modification of the descent direction.

The normalized steepest descent direction is defined as \[ \Delta x_{nsd} = \text{argmin}_x \{\nabla f(x)^T v : \|v\| = 1\} \] for some norm \(\|\cdot \|\).

Note: Steepest descent with the standard norm (\(\|\cdot\|_2\)) is the same as gradient descent.

Steepest descent algorithm

The same as gradient descent, but with a different descent direction:

Start with a point \(x\)

Repeat

\(\Delta x \leftarrow \Delta x_{sd}\).
Line search: Choose step size \(t\) by either backtracking line search or exact line search.
Update: \(x \leftarrow x + t \Delta x_{sd}\)

Until the stopping criterion is satisfied, usually \(\|\nabla f(x)\|_2 \le \epsilon\).

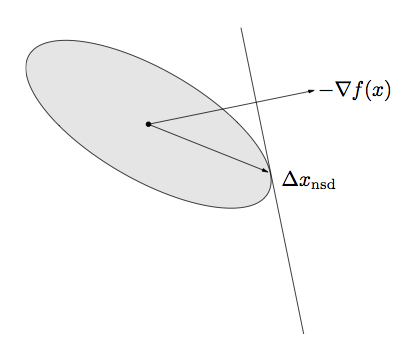
Normalized steepest descent direction for a quadratic norm

Ellipse is the set \(\{v: \|v\|_P \le 1\}\)
\(\Delta x_{nsd}\) is the point in the ellipse that extends farthest in the direction of \(-\nabla f(x)\).
Analytic solution for the steepest descent direction: \[ \Delta x_{nsd} = -(\nabla f(x)^T P^{-1} \nabla f(x))^{-1/2} P^{-1} \nabla f(x) \]
There is a standard way of normalizing, involving a dual norm (see the text if you're interested), the unnormalized steepest descent search direction is \[ \Delta x_{sd}= -P^{-1} \nabla f(x) \]

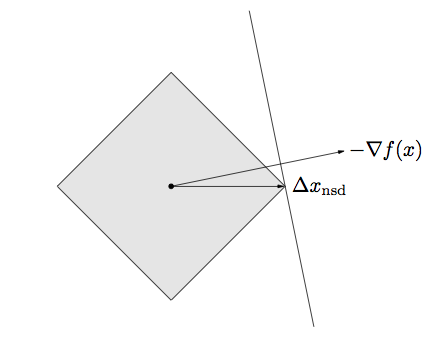
Normalized steepest descent direction for the \(\ell_1\) norm

Ellipse is the set \(\{v: \|v\|_1 \le 1\}\)
\(\Delta x_{nsd}\) is the point in norm ball that extends farthest in the direction of \(-\nabla f(x)\).

Examples of the effect of the norm

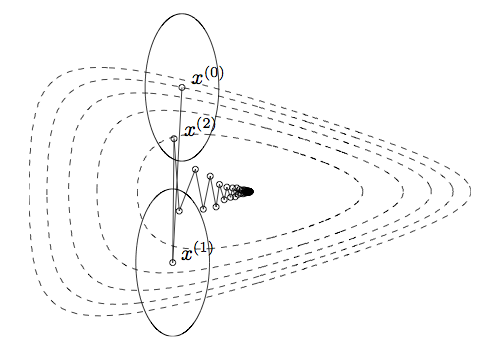
The choice of norm changes dramatically the number of steps needed to reach the optimum
Steps show steepest descent/backtracking line search for quadratic norms
Ellipses are the norm balls around each of the iterates

When can we expect these methods to do well?

From the pictures, we saw that

Gradient descent doesn't do well when the sublevel sets are far from spherical
Steepest descent does well when the norm balls approximate the sub-level sets.

Condition number of convex sets

Let \(C \subseteq \mathbb R^n\), and let \(q\) be a vector in \(\mathbb R^n\) specifying a direction.

The width of \(C\) in the direction \(q\) is \(W(C, q) = \sup_{z \in C} q^T z - \inf_{ \in C}q^T z\).
The minimum width and maximum width of \(C\) are \[ W_{min} = \inf_{\|q\|_2 = 1} W(C, q) \] and \[ W_{max} = \sup_{\|q\|_2 = 1} W(C, q) \]
The condition number of a convex set \(C\) is \(\text{cond}(C) = \frac{W_{max}^2}{W_{min}^2}\).
Measure of how far from spherical the set is.

Convergence bounds and condition number

Recall for gradient descent we had the following result: if \(f\) is strongly convex, \[ f(x^{(k)}) - p^\star \le c^k (f(x^{(0)}) - p^\star) \] where \(x^{(k)}\) is the \(k\)th gradient descent iterate.

The constant \(c\) depends on the maximum condition number of the sublevel sets of \(f\)
Large condition number corresponds to larger \(c\)
Small condition number corresponds to smaller \(c\).

Quadratic norms as a gradient descent in a transformed coordinate system

The quadratic norm \(\|\cdot\|_P\) is defined as \(\|x\|_P = x^T P x\), where \(P\) is a positive definite matrix.

Steepest descent with the \(\|\cdot\|_P\) norm is the same as gradient descent after a change of coordinates:

Let \(\bar u = P^{1/2} u\)
\(\|u\|_P = \|\bar u\|_2\)
\(\bar f(\bar u) = f(P^{-1/2} \bar u) = f(u)\)
Applying gradient descent to \(\bar f\) is equivalent to applying steepest descent with the \(\|\cdot\|_P\) norm to \(f\).

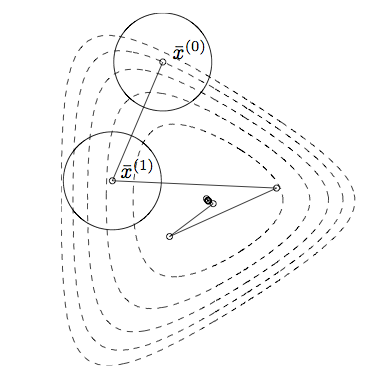
For example

Gradient descent on a transformed version of the problem before.
Sublevel sets now much closer to spherical, and the algorithm converges quickly.

Re-interpretation of Newton's method

Recall the Newton step: \(-\nabla^2 f(x)^{-1} \nabla f(x)\)
This search direction is the same as the steepest descent direction in the Hessian norm: \(\|\cdot\|_{\nabla^2 f(x)}\)
Turns out the Hessian norm gives a good approximation of the contours of the sublevel sets around the optimal point: this is why it has such fast convergence.