Stat 470/670 Lecture 23: Principal Components
Julia Fukuyama
A contrived example
Suppose we have a 3-dimensional object that we want to
investigate.
Due to some strange set of constraints, we are only allowed to see
its shadow.
Without knowing anything about the object, what sort of a shadow
would you expect to be most useful?
It seems like the most useful shadow is the biggest one: If we were
only allowed one view, we would ask for the one that took up the most
space.
It’s easy to come up with examples where this isn’t the most useful,
but it’s a good place to start if you don’t know anything about the
data.
The same will be true of PCA.
PCA as variance maximization
In PCA, we have a data matrix \(\mathbf X
\in \mathbb R^{n \times p}\) with centered columns.
We think of the rows of \(\mathbf
X\) as points in \(p\)-dimensional space, and we want to
project the points down into a lower-dimensional space so we can
visualize them.
There are a lot of different ways we could do this, but in PCA we
want to find the projection that maximizes the variance of the projected
points.
The PCA optimization problem
First consider projecting the points onto a line.
The PCA problem is to find \[
\mathbf w_{(1)} = \text{arg max}_{\mathbf w : \|\mathbf w \| = 1}
\sum_{i=1}^n (\mathbf x_i \cdot \mathbf w)^2
\] where \(\mathbf x_i\) is the
\(i\)th row of \(\mathbf X\).
\(\mathbf w_{(1)}\) is then the
first principal component.
If we want projections into higher-dimensional spaces, we take more
principal components.
We find the \(k\)th principal
component as \[
\mathbf w_{(k)} = \text{arg max}_{\mathbf w :\| \mathbf w \| = 1,
\mathbf w^T \mathbf w_{(j)} = 0, j = 1, \ldots, k-1} \sum_{i=1}^n
(\mathbf x_i \cdot \mathbf w)^2
\]
The constraint that \(\mathbf w^T \mathbf
w_{(k)} = 0, j = 1,\ldots, k-1\) means that the \(k\)th principal component is orthogonal to
all the previous principal components, and is needed to ensure a unique
solution to the problem.
Solution to the PCA problem
The solution to the PCA is given by the SVD.
If \(\mathbf X\) has centered
columns and \(\mathbf X = \mathbf U \mathbf D
\mathbf V^T\) is the SVD of \(\mathbf
X\), then
- The \(k\)th principal component is
the \(k\)th column of \(\mathbf V\).
- The projections of the points onto the \(k\)th principal component are given by the
\(k\)th row of \(\mathbf U \mathbf D\).
Example
library(devtools)
install_github("vqv/ggbiplot")
library(ade4)
library(ggbiplot)
## Loading required package: plyr
## Loading required package: scales
## Loading required package: grid
## Loading required package: viridisLite
##
## Attaching package: 'viridis'
## The following object is masked from 'package:scales':
##
## viridis_pal
Olympic dataset
data(olympic)
summary(olympic$tab)
## 100 long poid haut
## Min. :10.62 Min. :6.220 Min. :10.27 Min. :1.790
## 1st Qu.:11.02 1st Qu.:7.000 1st Qu.:13.15 1st Qu.:1.940
## Median :11.18 Median :7.090 Median :14.12 Median :1.970
## Mean :11.20 Mean :7.133 Mean :13.98 Mean :1.983
## 3rd Qu.:11.43 3rd Qu.:7.370 3rd Qu.:14.97 3rd Qu.:2.030
## Max. :11.57 Max. :7.720 Max. :16.60 Max. :2.270
## 400 110 disq perc
## Min. :47.44 Min. :14.18 Min. :34.36 Min. :4.000
## 1st Qu.:48.34 1st Qu.:14.72 1st Qu.:39.08 1st Qu.:4.600
## Median :49.15 Median :15.00 Median :42.32 Median :4.700
## Mean :49.28 Mean :15.05 Mean :42.35 Mean :4.739
## 3rd Qu.:49.98 3rd Qu.:15.38 3rd Qu.:44.80 3rd Qu.:4.900
## Max. :51.28 Max. :16.20 Max. :50.66 Max. :5.700
## jave 1500
## Min. :49.52 Min. :256.6
## 1st Qu.:55.42 1st Qu.:266.4
## Median :59.48 Median :272.1
## Mean :59.44 Mean :276.0
## 3rd Qu.:64.00 3rd Qu.:286.0
## Max. :72.60 Max. :303.2
oly_noscale = prcomp(olympic$tab, scale. = FALSE)
oly_noscale$rotation[,1:2]
## PC1 PC2
## 100 -0.0045042348 0.005632863
## long 0.0084964324 -0.013772028
## poid -0.0294931259 -0.155510542
## haut 0.0007153041 -0.002667193
## 400 -0.0455887408 -0.001324105
## 110 -0.0050441978 0.010836485
## disq -0.1184059716 -0.352166545
## perc 0.0003427802 -0.019704006
## jave -0.0525411029 -0.917592971
## 1500 -0.9900266310 0.095301595
PCA Biplots
Two types of biplots, form and covariance. Let’s
start off with the form biplot.
- For each sample we plot a point with the sample scores along the
principal axes.
- For each variable, we make an arrow with the variable weights along
the principal axes.
This allows us to read off the sample scores along the principal axes
and the variable weights along the principal axes.
However, there’s another way to interpret the PCA biplot:
- Since the PCA solution is given by the SVD, the biplot is the same
as the reduced-rank biplot (up to choices of how to scale the biplot
points and biplot axes).
- In particular, the form biplot is a reduced-rank biplot where we use
\(\mathbf U_{(2)} \mathbf D_{(2)}\) to
plot the biplot points, and \(\mathbf
V_{(2)}\) to plot the biplot axes.
- Therefore, we can read the PCA biplot as giving us an approximation
to the centered data matrix \(\mathbf
X\)
PCA biplot for the olympic data
## scale = 0 means form biplot
ggbiplot(oly_noscale, scale = 0) + ylim(c(-17, 10))
Covariance biplot
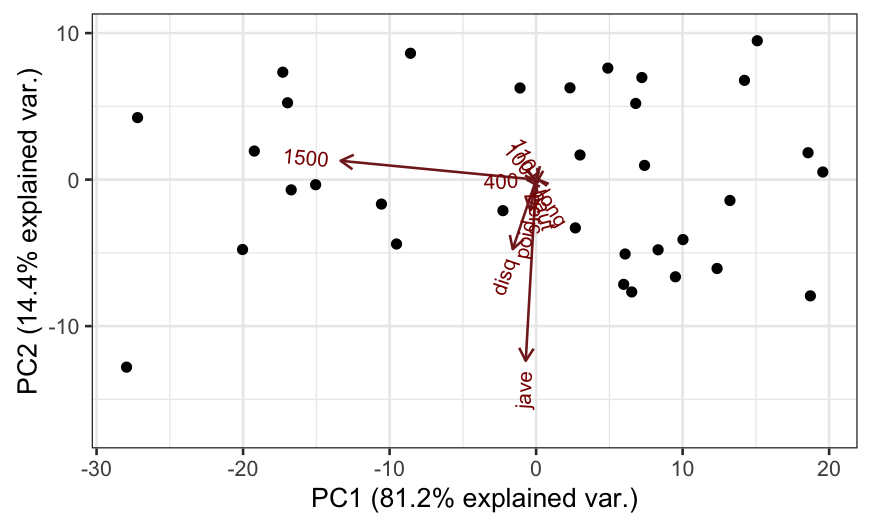
The covariance biplot is very subtly different from the form
biplot, the difference being how the singular values are allocated.
In the covariance biplot, we use
- \(\mathbf U_{(2)}\) for the biplot
points
- \(\mathbf V_{(2)} \mathbf D_{(2)}\)
for the biplot axes.
In this form of the biplot, angles between biplot axes give us
approximations of the covariances.
Why is this?
Following up on what we talked about regarding correlations between
variables, note the following two relationships:
- If \(\mathbf X\) has centered
columns, then \(\mathbf X^T \mathbf X\)
is proportional to the sample covariance matrix.
- If \(\mathbf X = \mathbf U \mathbf D
\mathbf V^T\), then \(\mathbf X^T
\mathbf X = \mathbf V \mathbf D^2 \mathbf V^T\).
Therefore, the columns of \(\mathbf V
\mathbf D\) can be seen as giving us both biplot points and
biplot axes for approximating the covariance matrix, and
projections of one biplot axis onto another biplot axis tells us about
the covariance between the two variables.
Covariance biplot
## scale = 1 means covariance biplot
ggbiplot(oly_noscale, scale = 1)
Correlation-based PCA
The example above suggests that doing PCA when the variables are on
different scales isn’t always that useful.
When the variables are on different scales and measure different
things, we often standardize the columns of \(\mathbf X\) (divide each column by its
standard deviation) before performing PCA.
This is sometimes referred to as correlation-based PCA, as opposed to
covariance-based PCA.
Correlation-based PCA biplot
Analogous to the covariance-based PCA biplot:
- Sample points represent the scores on the principal axes.
- Variable points represent variable weights on the principal
axes.
Interpretation as a reduced-rank biplot:
- Correlation-based PCA biplot is just a reduced-rank biplot
approximating a centered and scaled data matrix.
- We still have biplot points and axes, and they describe the elements
of the centered and scaled data matrix.
Relationships between the variables:
- Projections of biplot axes onto each other now describe correlations
between variables instead of covariances.
Covariance PCA biplot based on correlations, with some extra
information:
oly_scale = prcomp(olympic$tab, scale. = TRUE)
## scale = 1 means covariance biplot
ggbiplot(oly_scale, scale = 1)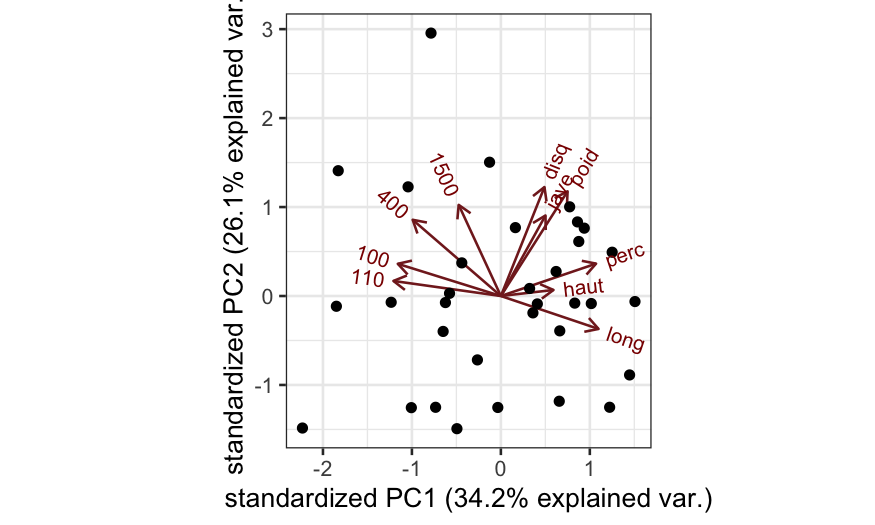
How would you interpret the first principal component?
Covariance PCA biplot based on correlations, with some extra
information:
## scale = 1 means covariance biplot
ggbiplot(oly_scale, scale = 1) +
geom_point(aes(color = olympic$score)) +
scale_color_viridis("Score")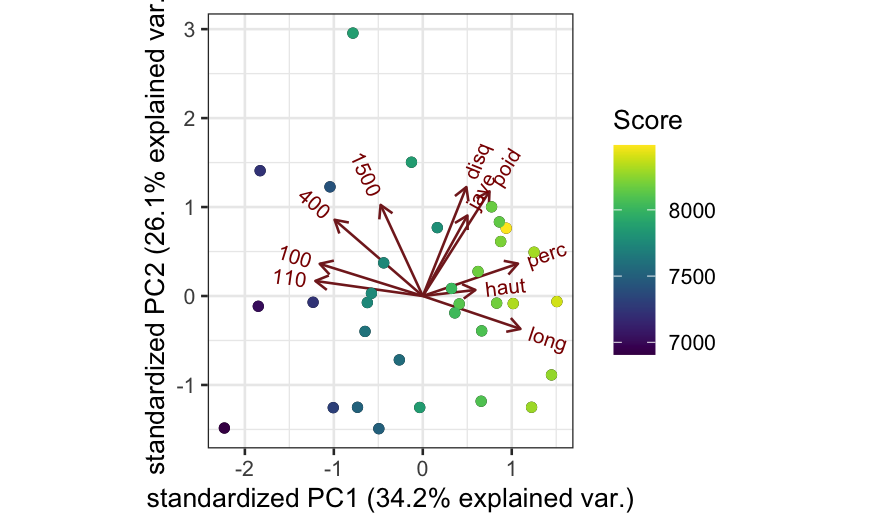
Wine example
Wine dataset
# ggbiplot is not on cran, so you have to use
# library(devtools)
# install_github("vqv/ggbiplot")
library(ggbiplot)
data(wine)
nrow(wine)
## [1] 178
## Alcohol MalicAcid Ash AlcAsh
## Min. :11.03 Min. :0.740 Min. :1.360 Min. :10.60
## 1st Qu.:12.36 1st Qu.:1.603 1st Qu.:2.210 1st Qu.:17.20
## Median :13.05 Median :1.865 Median :2.360 Median :19.50
## Mean :13.00 Mean :2.336 Mean :2.367 Mean :19.49
## 3rd Qu.:13.68 3rd Qu.:3.083 3rd Qu.:2.558 3rd Qu.:21.50
## Max. :14.83 Max. :5.800 Max. :3.230 Max. :30.00
## Mg Phenols Flav NonFlavPhenols
## Min. : 70.00 Min. :0.980 Min. :0.340 Min. :0.1300
## 1st Qu.: 88.00 1st Qu.:1.742 1st Qu.:1.205 1st Qu.:0.2700
## Median : 98.00 Median :2.355 Median :2.135 Median :0.3400
## Mean : 99.74 Mean :2.295 Mean :2.029 Mean :0.3619
## 3rd Qu.:107.00 3rd Qu.:2.800 3rd Qu.:2.875 3rd Qu.:0.4375
## Max. :162.00 Max. :3.880 Max. :5.080 Max. :0.6600
## Proa Color Hue OD
## Min. :0.410 Min. : 1.280 Min. :0.4800 Min. :1.270
## 1st Qu.:1.250 1st Qu.: 3.220 1st Qu.:0.7825 1st Qu.:1.938
## Median :1.555 Median : 4.690 Median :0.9650 Median :2.780
## Mean :1.591 Mean : 5.058 Mean :0.9574 Mean :2.612
## 3rd Qu.:1.950 3rd Qu.: 6.200 3rd Qu.:1.1200 3rd Qu.:3.170
## Max. :3.580 Max. :13.000 Max. :1.7100 Max. :4.000
## Proline
## Min. : 278.0
## 1st Qu.: 500.5
## Median : 673.5
## Mean : 746.9
## 3rd Qu.: 985.0
## Max. :1680.0
wine.pca = prcomp(wine, scale. = TRUE)
wine.pca$rotation[, 1:2]
## PC1 PC2
## Alcohol -0.144329395 0.483651548
## MalicAcid 0.245187580 0.224930935
## Ash 0.002051061 0.316068814
## AlcAsh 0.239320405 -0.010590502
## Mg -0.141992042 0.299634003
## Phenols -0.394660845 0.065039512
## Flav -0.422934297 -0.003359812
## NonFlavPhenols 0.298533103 0.028779488
## Proa -0.313429488 0.039301722
## Color 0.088616705 0.529995672
## Hue -0.296714564 -0.279235148
## OD -0.376167411 -0.164496193
## Proline -0.286752227 0.364902832
## PC1 PC2
## [1,] -3.307421 1.4394023
## [2,] -2.203250 -0.3324551
## [3,] -2.509661 1.0282507
## [4,] -3.746497 2.7486184
## [5,] -1.006070 0.8673840
## [6,] -3.041674 2.1164309
## [7,] -2.442201 1.1715453
## [8,] -2.053644 1.6044371
## [9,] -2.503811 0.9154885
## [10,] -2.745882 0.7872170
principal_axes = data.frame(wine.pca$rotation)
scores = data.frame(wine.pca$x)
ggplot(principal_axes) + geom_segment(aes(x = PC1, y = PC2, xend = 0, yend = 0))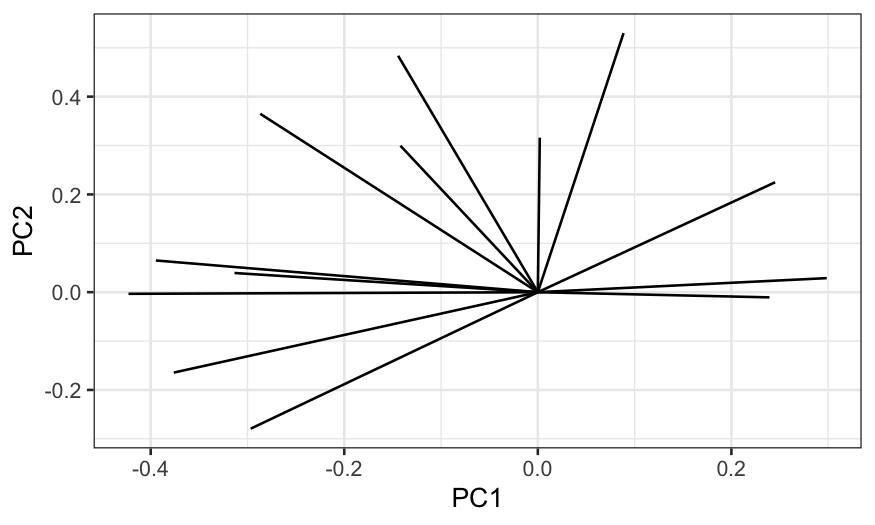
ggplot(scores) + geom_point(aes(x = PC1, y = PC2))
ggbiplot(wine.pca, scale = 1, var.axes = FALSE, groups = wine.class)
ggbiplot(wine.pca, scale = 1, var.axes = TRUE, groups = wine.class) + xlim(c(-2.5, 3))
Summing up
Interpretation of PCA:
- Visualization of the elements of the matrix
- Visualization of the correlation/covariance among the variables
Two kinds of PCA:
- Covariance-based PCA: columns of the data matrix are centered but
not scaled, implemented with
scale. = FALSE in
prcomp (the default)
- Correlation-based PCA: columns of the data matrix are centered and
scaled, implemented with
scale. = TRUE in
prcomp
Two kinds of PCA biplot:
- Form biplot: Plot \(\mathbf U_{(2)}
\mathbf D_{(2)}\) and \(\mathbf
V_{(2)}\), implemented with
scale = 0 in
ggbiplot
- Covariance biplot: Plot \(\mathbf
U_{(2)}\) and \(\mathbf V_{(2)} \mathbf
D_{(2)}\), implemented with
scale = 1 in
ggbiplot
