The basics/Our goals

Goals:

Describe a single univariate dataset.
Compare a univariate dataset to a reference distribution or to another univariate dataset.
Compare many univariate datasets.

Even if you have multivariate data, you should start out looking at the variables one by one, as if they were univariate.

Describing a single univariate dataset

Empirical CDF definition:

Let \(x_1, \ldots, x_n\) be our dataset.

The empirical cumulative distribution function (ecdf) is defined as \[ \text{ecdf}(x) = \frac{\text{\# of elements in the dataset with value } \le x}{\text{\# of elements in the dataset}} \]

Properties:

The function is monotone increasing.
Regions in which the curve is steep \(\leftrightarrow\) regions of high density.
Regions in which the curve is flat \(\leftrightarrow\) regions of low density.
Can easily read off the fraction of points in an interval from the function.
Assuming the samples are exchangeable, there is no loss of information going from the original dataset to the ecdf.

Let’s try this out in R

## lattice has the singer data that we're going to use
library(lattice)
library(ggplot2)
library(dplyr)
library(magrittr)
library(stringr)

Let’s try out ggplot

## nothing gets plotted! why not?
ggplot(singer, aes(x = height))

## we need to tell it not just that we want to plot height, but how to plot it. here we're saying to plot height as an ecdf
ggplot(singer, aes(x = height)) + stat_ecdf()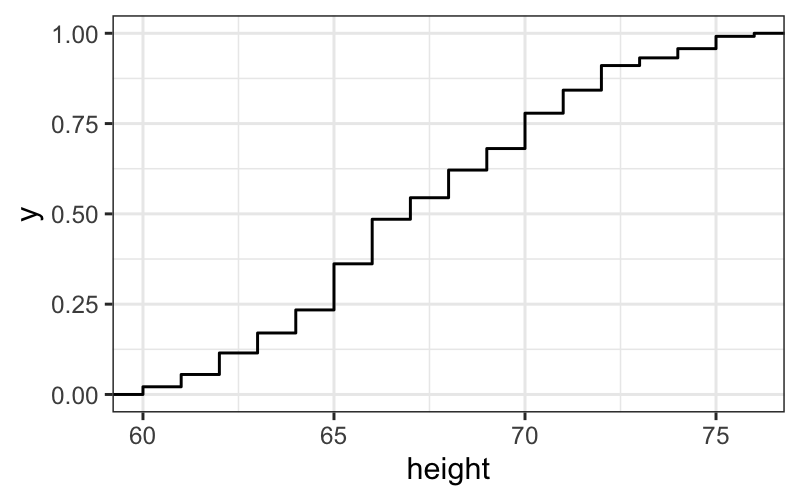

## another way of doing the same thing, ggplots can come in pieces
singer.gg = ggplot(singer, aes(x = height))
singer.gg + stat_ecdf()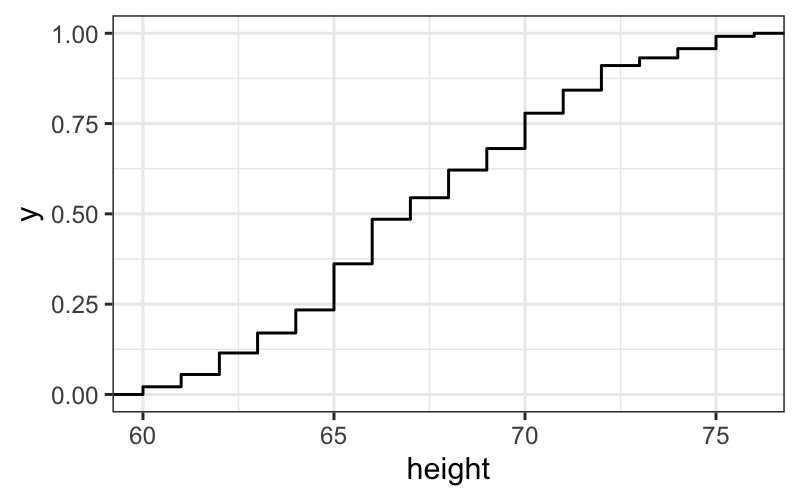

## and if we want to label the axes
singer.gg + stat_ecdf() +
    xlab("This is the x-axis") +
    ylab("This is the y-axis") + 
    ggtitle("Here's a title")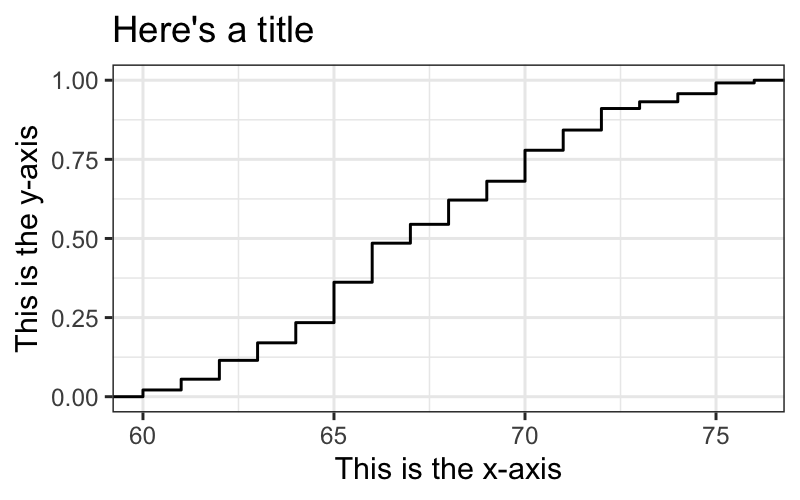

Other interpretations of the ECDF

Let \(X\) be a random variable obtained by drawing uniformly at random from the dataset \(x_1, \ldots, x_n\).

\[ \text{ecdf}(x) = P(X \le x) \]

Why is the ECDF a good representation of the data?

Remember from your other statistics courses the definition of a cumulative distribution function:

Let \(X\) be a random variable taking values in \(\mathbb R\), the cumulative distribution function \(F_X\) is defined as \[ F_X(x) = P(X \le x) \]

The empirical CDF is the analogous quantity for our data, and is the nonparametric maximum likelihood estimate of the population CDF.

Histograms and Density Estimates

Histogram: Definition

Let \(x_{(1)}, \ldots, x_{(n)}\) be the ordered data.

Set a number of bins \(m\).
Let \(r = x_{(n)} - x_{(1)}\).
Create \(m\) equally sized intervals: \(I_i = [x_{(1)} + \frac{r(i - 1)}{m}, x_{(1)} + \frac{ri}{m} )\)
For each \(i = 1,\ldots, m\), let \(c_i = \#\{ j : x_j \in I_i\}\).
For each interval \(I_i\), plot a bar with height \(c_i\), width \(r / m\), centered around \(x_{(1)} + \frac{r(i-1)}{m}\).

Histogram/Density estimate demonstration

ggplot(singer, aes(x = height)) + geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.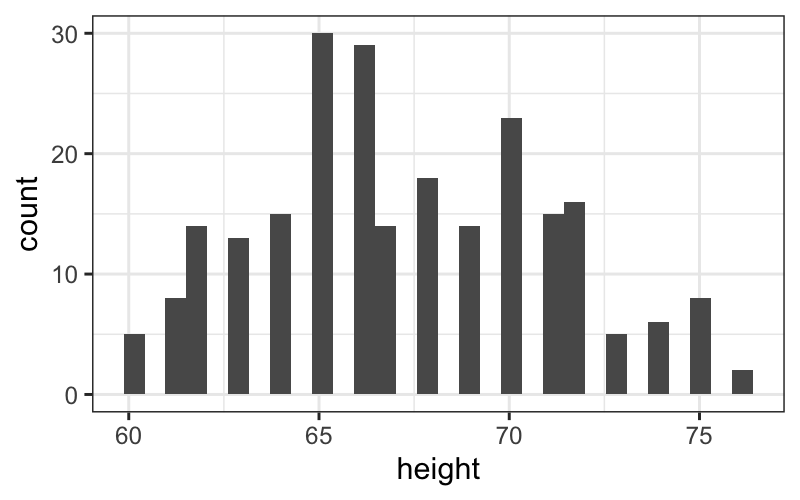

ggplot(singer, aes(x = height)) + geom_density()

ggplot(singer, aes(x = height)) +
    geom_density(adjust = .5) +
    geom_rug(aes(y = 0), sides = "b",
             position = position_jitter(height = 0))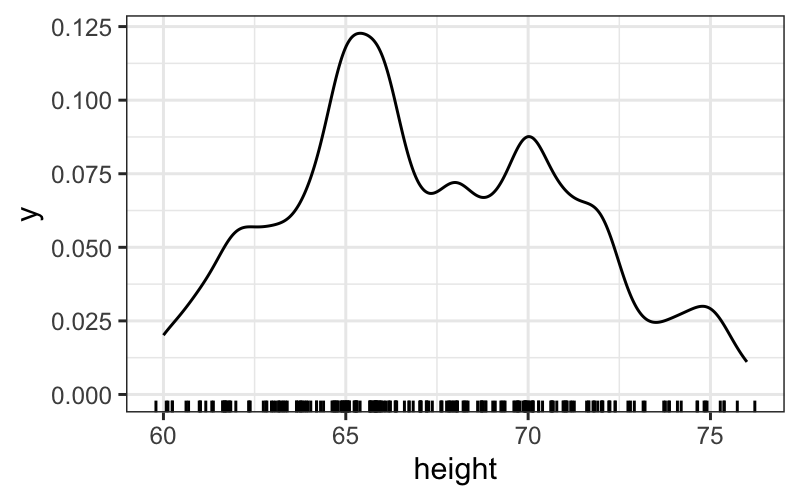

Exercise: play around with the jittering on the rug and the adjust parameter in the density. What do you like best? Again, try faceting out the histograms or plotting them over one another. Do different versions bring out different features of the data? What do you notice in the different plots?

set.seed(0)
df = data.frame(x = c(rnorm(25, 0, 1), rnorm(25, 5, 1)))
ggplot(df) + geom_histogram(aes(x = x))

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.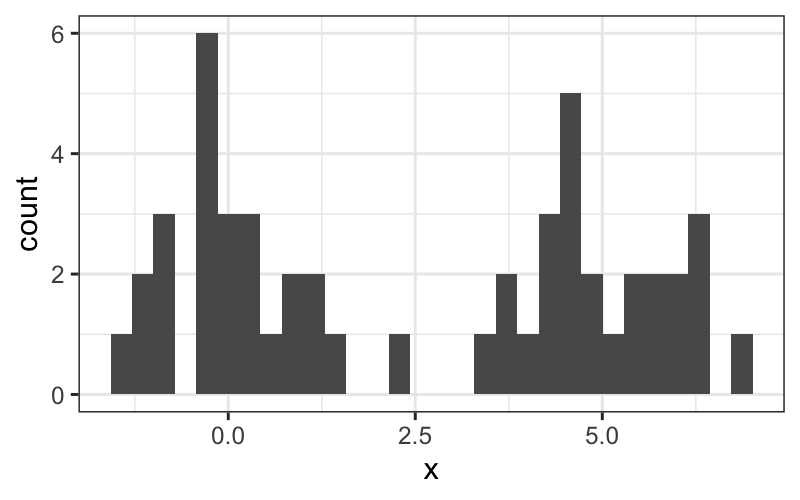

ggplot(df) + geom_histogram(aes(x = x), bins = 50)

ggplot(df) + stat_ecdf(aes(x = x))

Drawbacks of histograms:

Can be sensitive to bin size.
Difficult to compare to each other.
You are implicitly imposing a model on the data, and this can be a poor fit.
Poor visualization/sensitive to noise when you don’t have much data.

Q-Q Plots

Goal: Compare two univariate samples to each other.

Before doing that, we need to define the quantile function.

Quantile function: Definition

The \(f\) quantile, \(q(f)\), of a set of data is a value with the property that approximately a fraction \(f\) of the data are less than or equal to \(q(f)\).

Note: This definition doesn’t completely specify the quantile function.

For concreteness, we use Cleveland’s definition of the quantile function:

Let \(x_1, \ldots, x_n\) be the data from the \(n\) samples.
Let \(x_{(1)}, \ldots, x_{(n)}\) be the ordered data, so that \(x_{(1)} \le x_{(2)} \le \cdots \le x_{(n)}\)
Let \(f_i = \frac{i - .5}{n}\)
Let \(q(f_i) = x_{(i)}\)

Now we have a partial specification of a quantile function.

Create the remainder by linear interpolation of the points we do have.

There isn’t a nice R function for making quantile plots using Cleveland’s definition, but we can still work it out by hand.

## quantile plots by hand
Tenor1 = singer %>%
    subset(voice.part == "Tenor 1") %>%
    arrange(height)
## exactly the same as
Tenor1 = arrange(
    subset(singer, voice.part == "Tenor 1"), height)
## close to the same as
sort(singer$height[singer$voice.part == "Tenor 1"])

##  [1] 64 64 65 66 66 66 67 67 68 68 68 69 70 70 71 71 72 72 73 74 76

nTenor1 = nrow(Tenor1)
f.value = (0.5:(nTenor1 - 0.5))/nTenor1
Tenor1$f.value = f.value

ggplot(Tenor1, aes(x = f.value, y = height)) +
    geom_line() +
    geom_point()

You can also use the quantile function:

f.values = seq(0,1,length.out = 100)
q.values = quantile(Tenor1$height, probs = f.values)
ggplot(data.frame(f.values, q.values)) + geom_line(aes(x = f.values, y = q.values))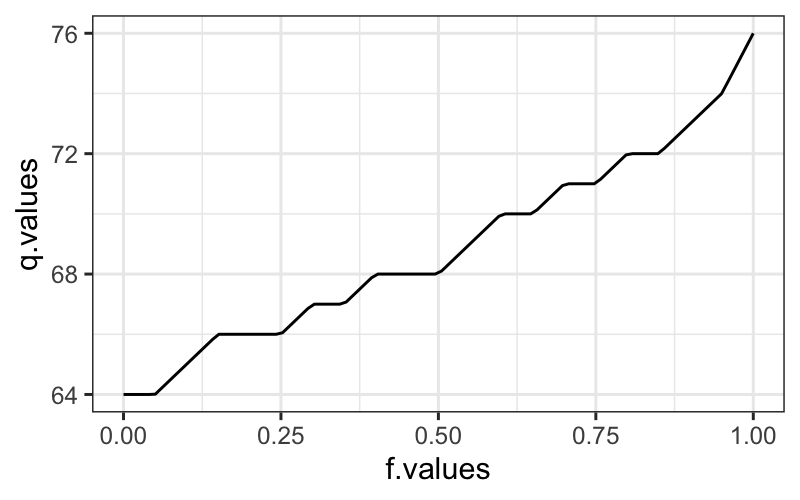

Quantile-Quantile (q-q) plot definition

Suppose we have two sets of univariate measurements, \(x_{(1)}, \ldots, x_{(n)}\) and \(y_{(1)}, \ldots, y_{(m)}\), with \(m \le n\).

For each \(i = 1,\ldots, m\), plot the \((i - .5) / m\) quantile of the \(y\) dataset against the \((i - .5) / m\) quantile of the \(x\) dataset.

Note:

If \(m = n\), then

\(q_x((i - .5) / m) = x_{(i)}\)
\(q_y((i - .5) / m) = y_{(i)}\) So in this case, we are simply plotting \(x_{(i)}\) against \(y_{(i)}\)

Q-Q plot demonstration

I will show three ways to make a QQ plot for two samples.

The simplest way is to use the qqplot function:

Tenor1 = singer %>% subset(voice.part == "Tenor 1")
Bass2 = singer %>% subset(voice.part == "Bass 2")
qqplot(Tenor1$height, Bass2$height)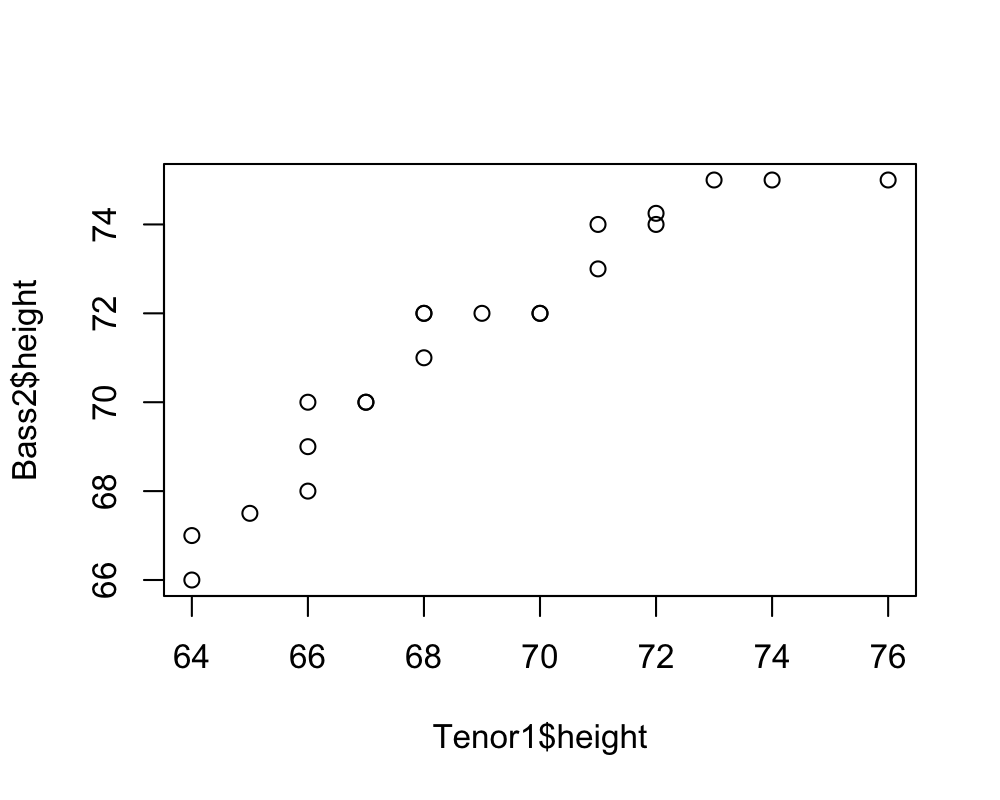

If you really want all your plots to be in ggplot, you can ask the qqplotfunction to return a data frame that you can plot with ggplot.

qq.df = as.data.frame(qqplot(Tenor1$height, Bass2$height,
    plot.it = FALSE))
ggplot(qq.df, aes(x = x, y = y)) +
    geom_point() +
    xlab("Tenor 1") + ylab("Bass 2")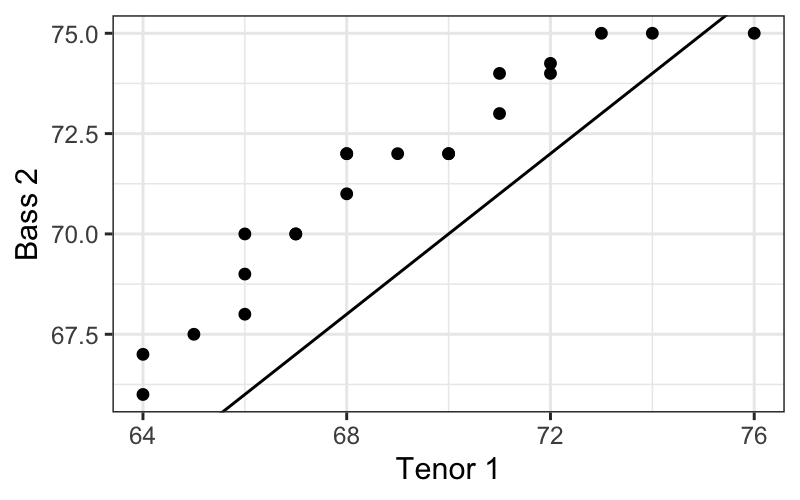

If you want to do it more “by hand,” you can use the quantile function to get the quantiles of both distributions and plot them against each other.

The quantile function seems to handle ties a bit differently than the qqplot function, but this should give quite similar results.

f.values = (0:(nrow(Tenor1) - 1)) / nrow(Tenor1)
q.values.tenor = quantile(Tenor1$height, probs = f.values)
q.values.bass = quantile(Bass2$height, probs = f.values)
ggplot(data.frame(q.values.tenor, q.values.bass)) + geom_point(aes(x = q.values.tenor, y = q.values.bass))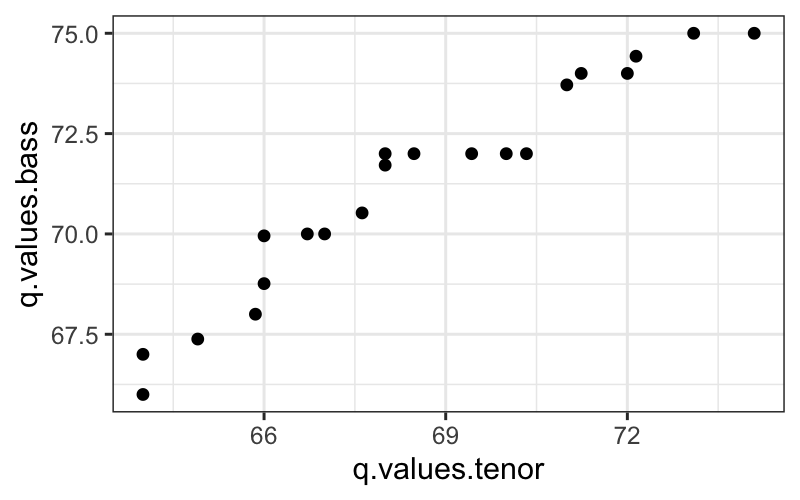

Alternative: compare two histograms or density estimates

Tenor1_or_Bass2 = singer %>% subset(voice.part %in% c("Tenor 1", "Bass 2"))
ggplot(Tenor1_or_Bass2) +
    geom_histogram(aes(x = height, fill = voice.part),
                   alpha = .5, position = "dodge")

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.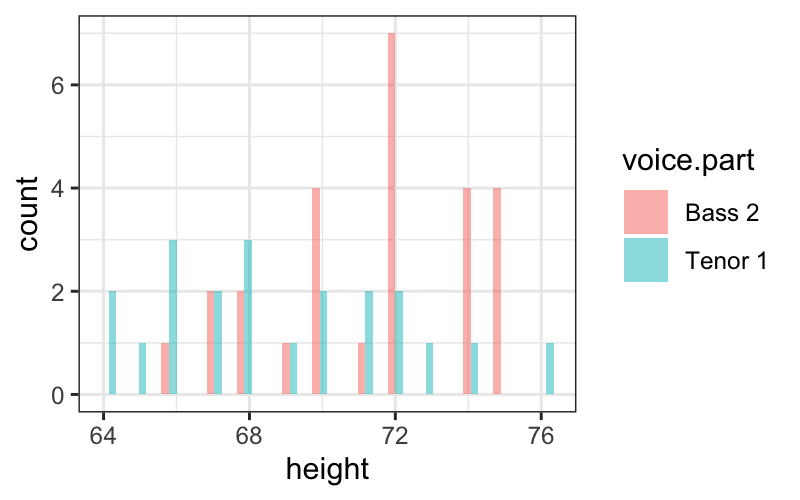

ggplot(Tenor1_or_Bass2) +
    geom_density(aes(x = height, fill = voice.part), alpha = .5)

Q-Normal plots

Goal: Check how well a normal distribution approximates the data

Definition: Theoretical quantiles

Let \[ q_{\mu, \sigma}(f) = \{ x : P(\mathcal N(\mu, \sigma^2) \le x = f) \} \]

In words: the value \(x\) such that the probability that a \(\mathcal N(\mu, \sigma^2)\) random variable takes value at most \(x\) is equal to \(f\).

Note the analogy to data quantiles, \(q_x(f)\) defined before.

Definition: Q-Normal plot

Let \(x_{(1)}, \ldots, x_{(n)}\) be our ordered data.

Recall that we defined the sample quantile function at values \(f_i = (i - .5) / n\) as \(q_x(f_i) = x_{(i)}\).

For each value \(f_i\), \(i = 1,\ldots, n\), compute

\(q_x(f_i)\), the sample quantile at \(f_i\)
\(q_{0,1}(f_i)\), the theoretical quantile for \(\mathcal N(0,1)\) at \(f_i\)

A Q-normal plot shows sample quantiles on the \(y\)-axis and theoretical quantiles on the \(x\)-axis.

Properties:

If the points lie along the line \(y = x\), the distribution is well approximated by a \(\mathcal N(0,1)\) distribution.
If the points lie along another straight line with intercept \(\mu\) and slope \(\sigma\), the distribution is well approximated by a \(\mathcal N(\mu, \sigma^2)\) distribution.
We can make the analogous plot to check how well our data is approximated by any distribution.
Q-Q plot (plotting the quantiles of two datasets) can be thought of as comparing the quantiles of one sample to an estimate of the distribution of the other sample.

Q-Normal plot demonstration

Let’s first see what a Q-normal plot looks like when the data really come from a normal distribution.

ggplot(data.frame(x = rnorm(100))) +
    stat_qq(aes(sample = x)) +
    geom_abline(aes(slope = 1, intercept = 0))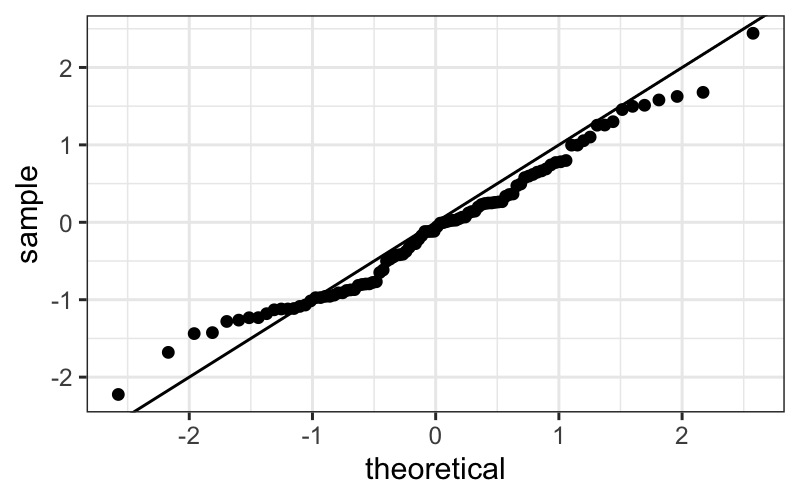

Then we have a reference for how closely to the line the points should lie when we’re looking at real data.

ggplot(singer) + stat_qq(aes(sample = height), distribution = qnorm)

Summing up

To visualize one distribution:

ECDF
Quantile plot
Density estimate
Histogram

To compare two distributions:

Q-Q plot
Overlay two of the single-distribution plots

To compare a distribution to a theoretical distribution:

Q-normal plot

Stat 470/670 Lecture 2: Univariate Data Visualization