Stat 470/670 Lecture 15: Binary data and logistic regression

Julia Fukuyama

Problem setup

We are interested in understanding voting patterns, and in particular how vote for president is related to income.

There is data on this topic in the ANES dataset: for each election, they have demographic information on a subset of voters plus information about how they voted in the presidential elections.

The variables here have particularly uninformative names, but the ones we are interested in describe the year, income, and presidential vote. They are coded as:

The primary difference between our task here and the modeling that we’ve done earlier in the semester is that the variable we’re trying to predict, vote, is binary. That is, it only takes two values (here vote for Republicans vs. vote for Democrats) instead of taking as a value any real number. This turns out to be enough of a difference that we need a new modeling technique.

Income is measured on a scale from 1 to 5:

1: 0 to 16 percentile

2: 17 to 33 percentile

3: 34 to 67 percentile

4: 68 to 95 percentile

5: 96 to 100 percentile

Using percentiles allows comparability between years. Also note that this is really an ordinal variable but we might find some advantages in treating it as quantitative.

ANES = read.csv("anes.csv")
income = ANES$VCF0114
summary(income)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    1.00    2.00    3.00    2.87    4.00    5.00    5449
table(income) / length(income)
## income
##          1          2          3          4          5 
## 0.15804751 0.15120779 0.29807821 0.25447084 0.04729414

Next we need the year for each observation. This is VCF0004.

year = ANES$VCF0004
summary(year)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1948    1970    1986    1985    2002    2016

The coding is that “1” means the Democrat, “2” means the Republican, and “0” or “NA” means some other outcome. We want everything to be coded as 0, 1, or NA (using 0/1 coding is the standard way to code binary variables for logistic regression).

vote = ANES$VCF0704a
##  First, change the zeroes to NA’s:
vote[vote == 0] = NA
## Then, to go from 2 representing Republican and 1 representing Democrat to 1 = Republican, 0 = Democrat, we just have to subtract 1
vote = vote - 1
summary(vote)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    0.00    0.00    0.00    0.48    1.00    1.00   35118

The variable really represents the fraction of the two-party vote that was for Republicans now, so for clarity let’s just rename it as such.

Republican = vote

Let’s put everything in a data frame, and then filter to just presidential election years:

ANES_df = data.frame(year, income, Republican)
ANES_df = filter(ANES_df, year %in% seq(1948, 2016, 4))
summary(ANES_df)
##       year          income        Republican   
##  Min.   :1948   Min.   :1.000   Min.   :0.000  
##  1st Qu.:1972   1st Qu.:2.000   1st Qu.:0.000  
##  Median :1992   Median :3.000   Median :0.000  
##  Mean   :1989   Mean   :2.861   Mean   :0.481  
##  3rd Qu.:2012   3rd Qu.:4.000   3rd Qu.:1.000  
##  Max.   :2016   Max.   :5.000   Max.   :1.000  
##                 NA's   :2524    NA's   :14394

Visualizing the relationship with one predictor

The first question we can ask is about the relationship between income and the probability of voting Republican in 1992. Let’s start off just by plotting the two points. It turns out that this isn’t trivial because the variables are categorical, and we need to do some work to get anything useful. Jittering helps with categorical variables, and we use it here:

ANES92 = subset(ANES_df, year == 1992)
ggplot(ANES92, aes(x = income, y = Republican)) +
    geom_point()

ggplot(ANES92, aes(x = income, y = Republican)) +
    geom_jitter(height = 0.1, width = 0.25, size = .7)

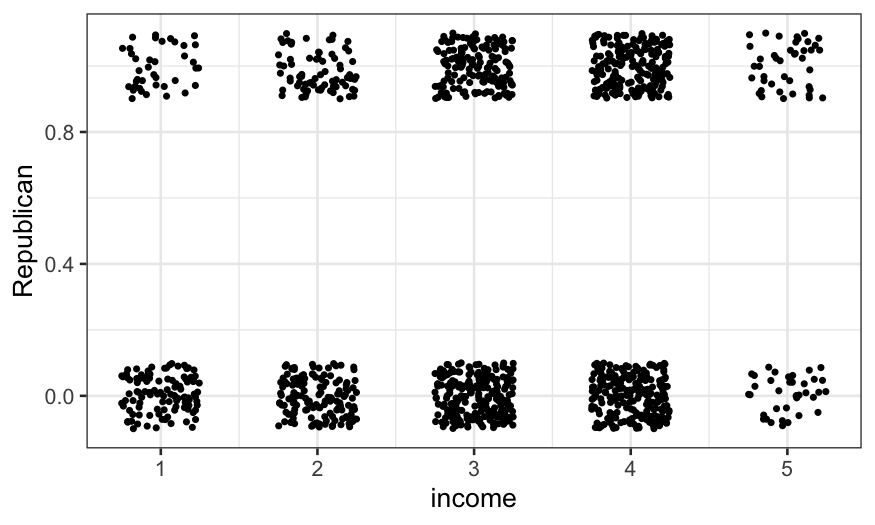
The jittered plot is ok, but here it’s actually more useful to compute the fraction of the vote going to Republicans and either look at the table or plot those values.

(republican_fraction_by_income = ANES92 %>%
     group_by(income) %>%
     summarise(republican_fraction = mean(Republican, na.rm = TRUE)))
## # A tibble: 6 × 2
##   income republican_fraction
##    <int>               <dbl>
## 1      1               0.267
## 2      2               0.345
## 3      3               0.404
## 4      4               0.488
## 5      5               0.532
## 6     NA               0.433
## zero values for income mean missing
ggplot(subset(republican_fraction_by_income, income != 0)) +
    geom_point(aes(x = income, y = republican_fraction))

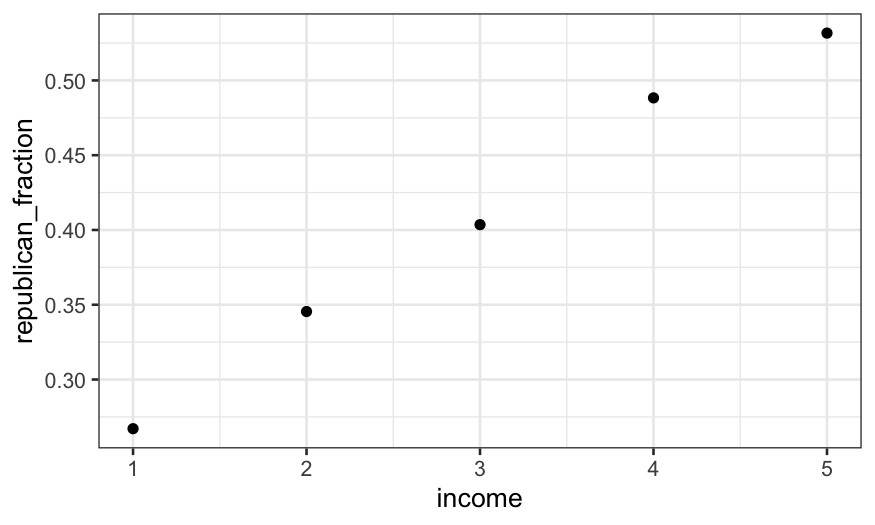
How could we model this relationship?

This gives the proportion (out of major party voters) who voted for Bush for each income group. Aside from group zero, which represents missing values of income, we see a strictly increasing pattern. How do we model this? Three options (not the only three) include:

  1. Linear regression with income as a numerical predictor.
  1. Logistic regression with income as a numerical predictor.
  1. Regression with income as a categorical (factor) predictor. (In this linear and logistic give identical predictions.)

Method 1 is the easiest to interpret: we get a slope that directly tells us the change in model probability of voting Republican as income goes up one category. However, linear regression for binary responses has two big limitations:

Method 3 isn’t really a model at all: it just returns the proportion within each category who voted for Bush, the same as our summarise() call gave us above. There’s something to be said for not fitting restrictive models when you don’t have to. However, if our goal is to fit more complex models or make comparisons between different sets of data, as it eventually will be, then some degree of simplification may be useful to understand the patterns in the data. Or we might fit a simplifying model first, then go back and look at the data in more detail and see if there are any important features our model missed. That will be our basic approach here.

Method 2, logistic regression, should work well. It does require treating a predictor that isn’t inherently a numeric variable as numeric, and requires a parametric form (effects are linear on a logit scale.) However, most of the time, doing this is reasonable as long as the pattern of the probability with \(x\) is monotonic and as long as predictive accuracy is not the sole goal.

Logistic regression with one predictor

We fit such a logistic regression using income as a quantitative variable and omitting missing values. Logistic regression is a special case of a GLM, so we use the glm() function; specifying a binomial family fits a logistic regression by default. Firstly, we can just add the fitted curve to the jittered plot:

ggplot(ANES92, aes(x = income, y = Republican)) +
    geom_jitter(height = 0.1, width = 0.25) +
    geom_smooth(method = "glm", method.args = list(family = "binomial"))
## `geom_smooth()` using formula = 'y ~ x'

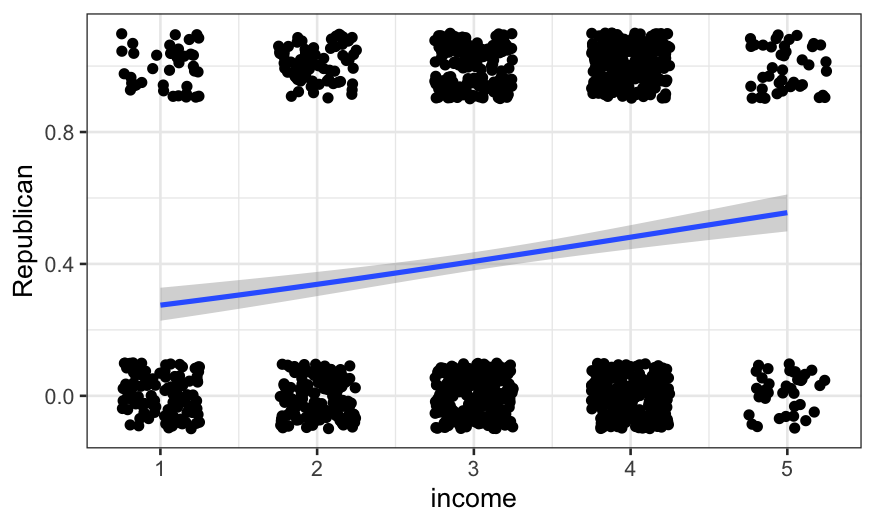
We can also fit it explicitly:

logit_92 = glm(Republican ~ income, family = binomial, data = ANES92)
summary(logit_92)
## 
## Call:
## glm(formula = Republican ~ income, family = binomial, data = ANES92)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.2733  -1.0235  -0.9086   1.2096   1.6069  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -1.26750    0.17789  -7.125 1.04e-12 ***
## income       0.29802    0.05379   5.541 3.01e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1719.1  on 1266  degrees of freedom
## Residual deviance: 1687.2  on 1265  degrees of freedom
##   (1218 observations deleted due to missingness)
## AIC: 1691.2
## 
## Number of Fisher Scoring iterations: 4

The summary gives a lot of information; we’ll focus on the coefficients. The summary tells us that

\[ \text{logit}[P(\text{Republican})]=−1.27+0.298\times \text{income} \]

where the logit function is

\[ \text{logit}(x)=\text{log}_e [x/(1−x)] \]

To find \(P(\text{Republican})\), we invert the logit:

\[ P(\text{Republican})=\text{logit}^{-1} (-1.27 + 0.298 \times \text{income}) \]

where \[ \text{logit}^{-1}(y) = \frac{e^y}{1+e^y} \]

For a quick and dirty interpretation, the “divide by 4” rule is useful: the maximum change in probability associated with a one unit change in \(x\) is the coefficient of \(x\) divided by four. So going one income group changes the model probability by up to about 7.5%. This looks like it’s about the increase in the curve from income group 4 to group 5.

We can check how good the approximation is:

## the package boot has the inv.logit function
library(boot)
## P(Republican) evaluated at income = 4
inv.logit(-1.27 + 0.298 * 4)
## [1] 0.4805099
## P(Republican) evaluated at income = 5
inv.logit(-1.27 + 0.298 * 5)
## [1] 0.5547792

Fitting a series of regressions

We’re not just interested in 1992. We want to know the relationship between income and vote for every Presidential election we have data for – is the relationship similar for every election, or are some elections different? Has there been a consistent change over time?

In programming terms, the easiest way to fit the same model on many subsets of the data is to write a function that subsets the data and fits the model, then to write a for loop to fit the model for each subset. There are much more computationally efficient approaches, but otherwise more efficiency usually isn’t worth the effort.

Here’s a function to fit our weighted logistic regression of vote on income for any given year.

logit_ANES_subset = function(my_year, data) {
    ## newdata = the subset of the data corresponding the year in question
    newdata = subset(data, year == my_year)
    ## model where the data are a subset corresponding to my_year
    model = glm(Republican ~ income, family = binomial, 
        data = newdata)
    ## getting just the output from the logistic regression fit that we need
    output = c(my_year, summary(model)$coef[2, 1:2])
    return(output)
}

The function returns the year, the model’s coefficient for income, and the standard error of that coefficient. We shouldn’t take the standard error too literally, because we haven’t accounted for the complex design of the ANES surveys.

Let’s test the function out on 1992 (Bush-Clinton).

logit_ANES_subset(my_year = 1992, data = ANES_df)
##                  Estimate   Std. Error 
## 1.992000e+03 2.980249e-01 5.378931e-02

Once we’ve checked that it works, we can loop over every presidential election year in our dataset: every four years between 1948 and 2012:

years = seq(1948, 2016, 4)
n = length(years)
income_by_year = data.frame(year = rep(NA, n), income_coef = rep(NA, n), income_se = rep(NA, n))
for (J in 1:n) {
    my_year = years[J]
    income_by_year[J, ] = logit_ANES_subset(my_year = my_year, data = ANES_df)
}

We’ll display the results using ggplot. geom_errorbar() lets us add one standard error bounds. We shouldn’t take these too literally, just use them to get a ballpark idea of uncertainty.

gg = ggplot(income_by_year, aes(x = year, y = income_coef, ymin = income_coef - 
    income_se, ymax = income_coef + income_se))
gg + geom_errorbar(width=1) + 
    ylab("Coefficient of income in linear model")

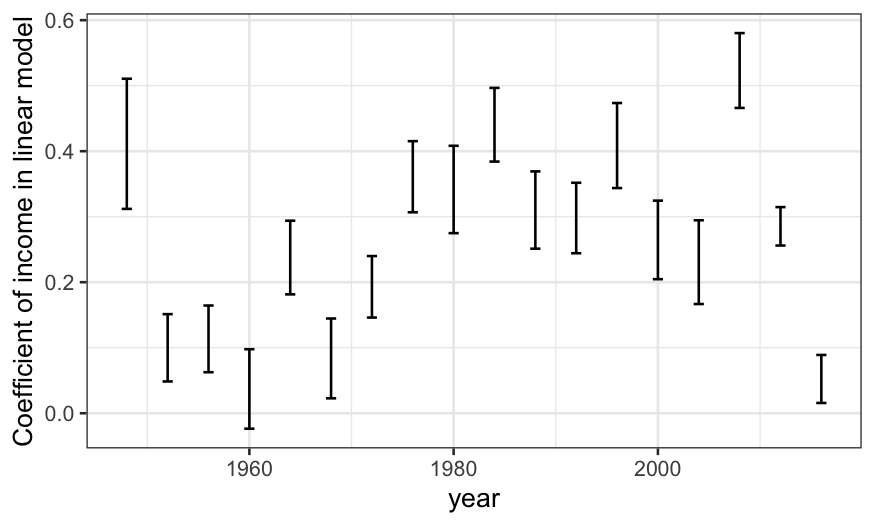
The income coefficient is positive for every election, meaning richer people were more likely to vote Republican every time (though 1960 was close.) The general trend was an increase in the income coefficient from 1952 to 1984, then a leveling-off. There was a huge drop from 1948 to 1952; unfortunately we don’t have data from before 1948 to know if the election was typical.

Less modeling, more detail

In our regressions, we treated income as a quantitative variable. A simpler approach would be to treat it as a factor, and simply track the weighted proportion of each income group that (two-party) voted Republican by year. Again, this is easiest to program (if inefficient) using a for loop.

To find means, I used use mean() in conjunction with summarise() in dplyr. Let’s first work out how to do it for the 1992 data.

summarise(group_by(ANES92, factor(income)), prop_Republican = mean(Republican, na.rm = TRUE))
## # A tibble: 6 × 2
##   `factor(income)` prop_Republican
##   <fct>                      <dbl>
## 1 1                          0.267
## 2 2                          0.345
## 3 3                          0.404
## 4 4                          0.488
## 5 5                          0.532
## 6 <NA>                       0.433
income_prop = ANES_df %>%
    group_by(income, year) %>%
    summarise(prop_Republican = mean(Republican, na.rm = TRUE))
## `summarise()` has grouped output by 'income'. You can override using the
## `.groups` argument.
## clean up a bit
income_prop = income_prop %>%
    ## making income an ordered factor will give a nice color scale for us later
    mutate(income_ord = factor(income, levels = 1:5, ordered = TRUE))
gg = ggplot(income_prop, aes(x = year, y = prop_Republican, group = income_ord, color = income_ord)) +
    geom_point() + geom_line()
gg + ylab("Proportion of two-party vote\nfor Republicans") + labs(color = "Income percentile")

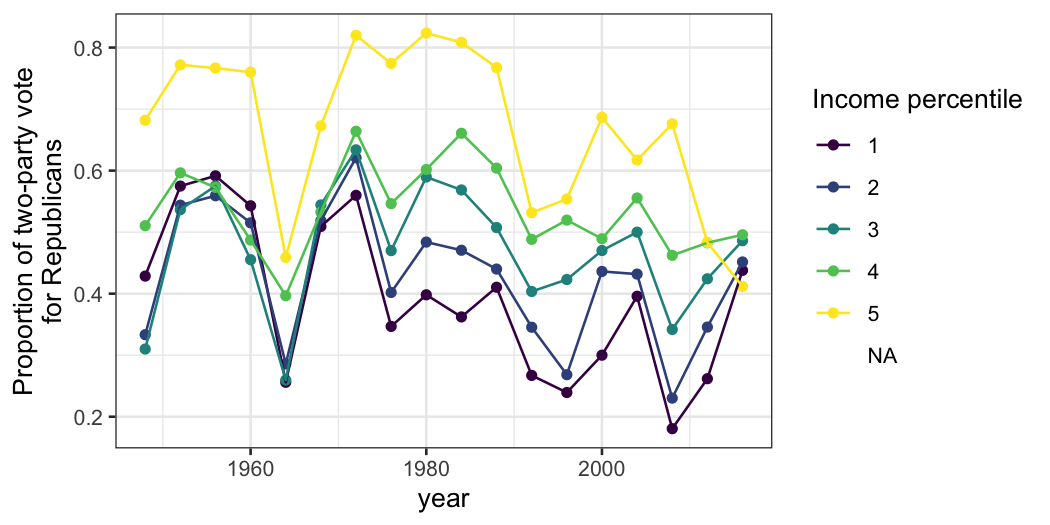
We now have a bit more detail on the trends and the aberrant results.

We can also draw lines to connect income groups by year. Because there are so many different years, we’ll facet them rather than color them.

ggplot(income_prop, aes(x = income, y = prop_Republican)) +
    geom_line() +
    facet_wrap(~ year, ncol = 6) + ylab("Proportion of two-party vote for Republican")

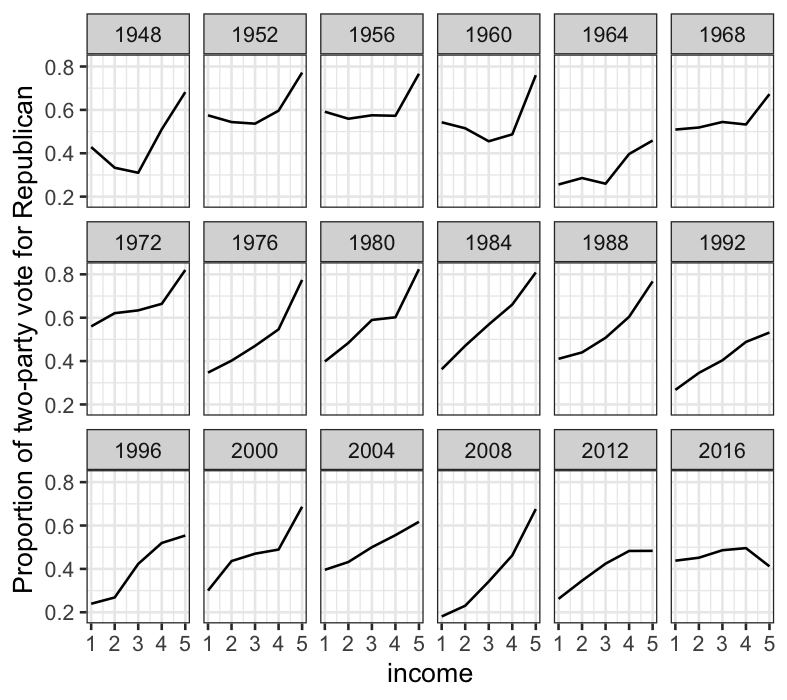
This yields less insight, but still has interesting features: notably the big magnitude of the uptick in Republicanism for the highest income group for almost every year.

Data summaries vs. data models

Both data summaries (like our last plot) and models (like our logistic regressions) have their uses.

In practice, going back and forth between models and data summaries, as we did here, is often very useful in exploratory work. Models can usefully simplify the data so you can get the big picture. Then you can look a fuller data summary and bear in results that the big picture doesn’t explain.