Pairs plot of the three variables
## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2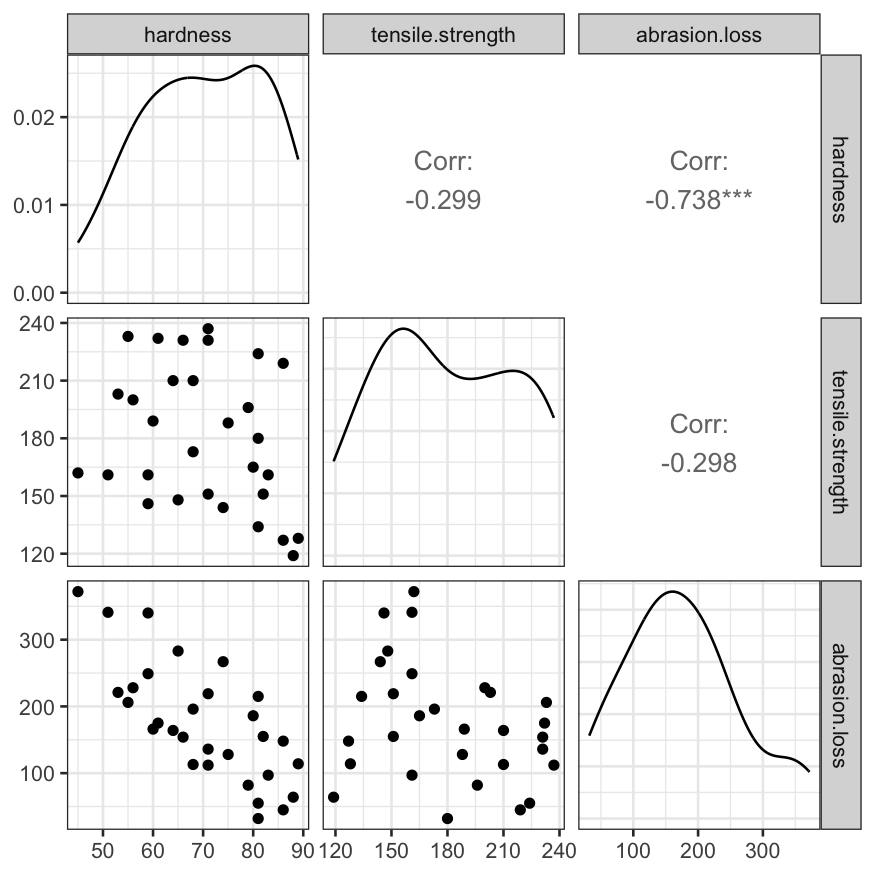
Julia Fukuyama
One more example with a slightly complicated model
Reading: Cleveland pp. 180-187, 200-213
The data frame rubber in lattice.RData contains three
measurements on 30 specimens of tire rubber.
The variables are:
hardness: How much the rubber rebounds after being
indented.tensile.strength: The force per cross-sectional area
required to break the rubber (in kg/cm2).abrasion.loss: The amount of material lost to abrasion
when rubbing it per unit energy (in grams per hp-hour). This gives you
an idea how fast the tire will wear away when you drive. If we had to
choose a “response” variable, it would be this one.## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2
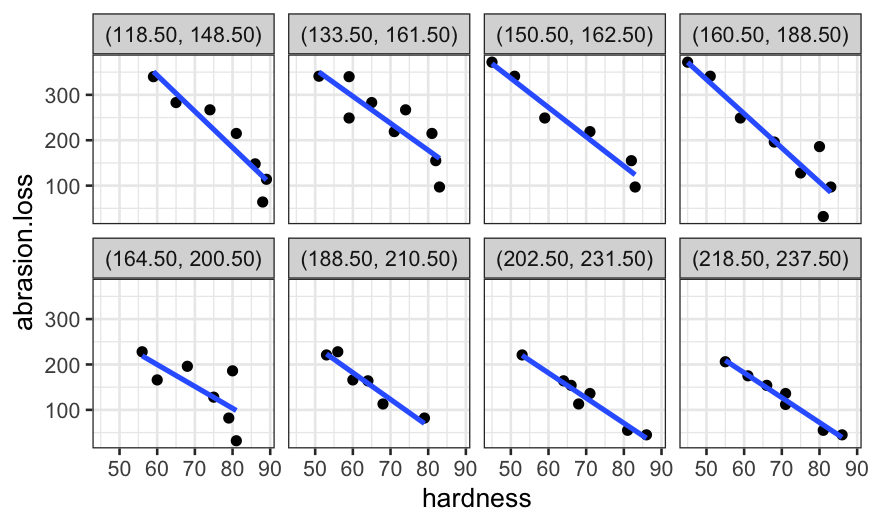
coplot_hardness = make_coplot_df(rubber, "hardness", number_bins = 8)
ggplot(coplot_hardness, aes(x = tensile.strength, y = abrasion.loss)) +
geom_point() +
facet_wrap(~ interval, ncol = 4) +
stat_smooth(method = "lm", se = FALSE)## `geom_smooth()` using formula = 'y ~ x'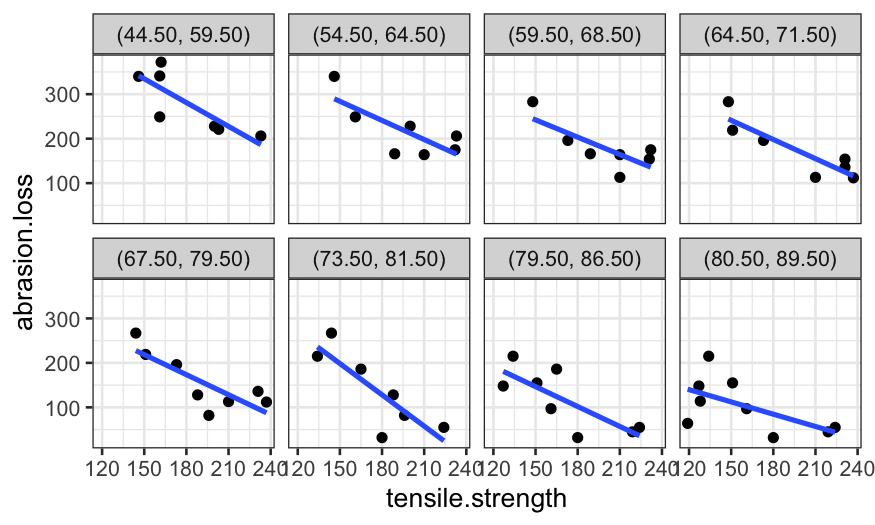
ggplot(coplot_hardness, aes(x = tensile.strength, y = abrasion.loss)) +
geom_point() +
facet_wrap(~ interval, ncol = 4) +
stat_smooth(method = "loess", method.args = list(degree = 1), se = FALSE)## `geom_smooth()` using formula = 'y ~ x'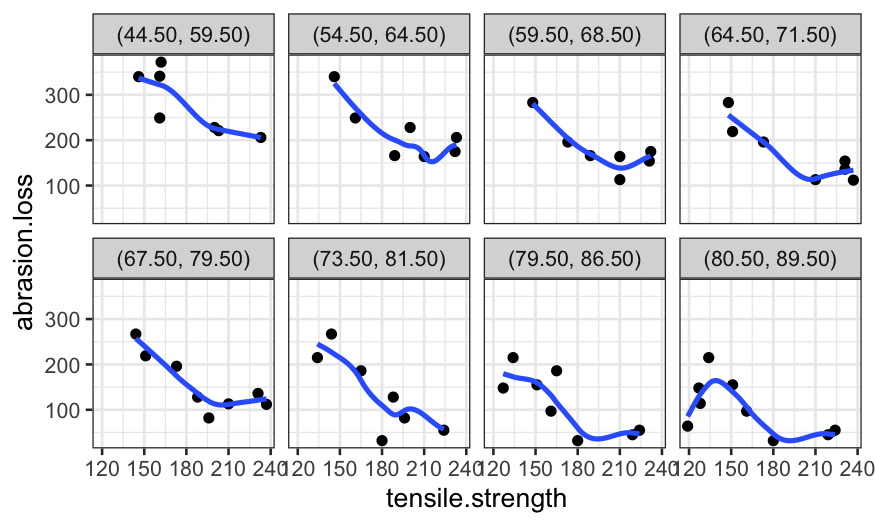
An easier way to make a coplot with ggplot is to use the
cut_number function:
ggplot(rubber, aes(x = tensile.strength, y = abrasion.loss)) +
geom_point() +
facet_grid(. ~ cut_number(hardness, n = 4)) +
stat_smooth(method = "loess", method.args = list(degree = 1, span = .9), se = FALSE)## `geom_smooth()` using formula = 'y ~ x'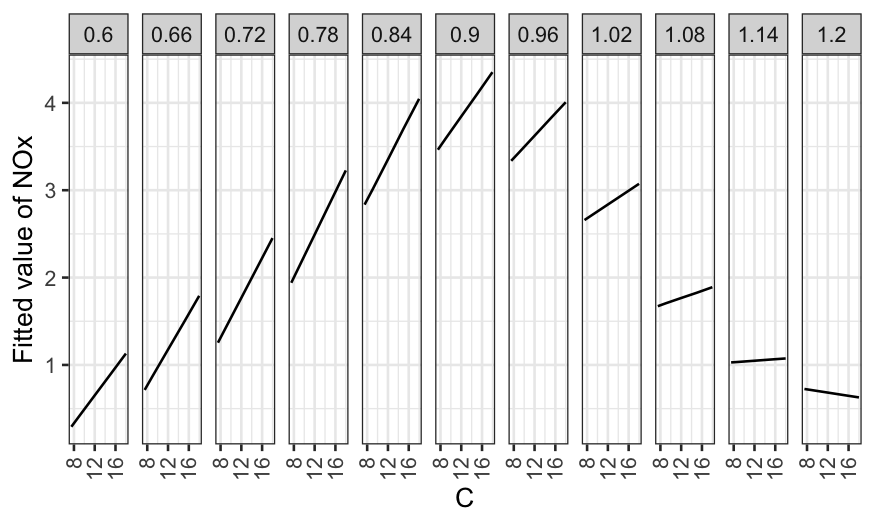
coplot_ts = make_coplot_df(rubber, "tensile.strength", number_bins = 8)
ggplot(coplot_ts, aes(x = hardness, y = abrasion.loss)) +
geom_point() +
facet_wrap(~ interval, ncol = 4) +
stat_smooth(method = "lm", se = FALSE)## `geom_smooth()` using formula = 'y ~ x'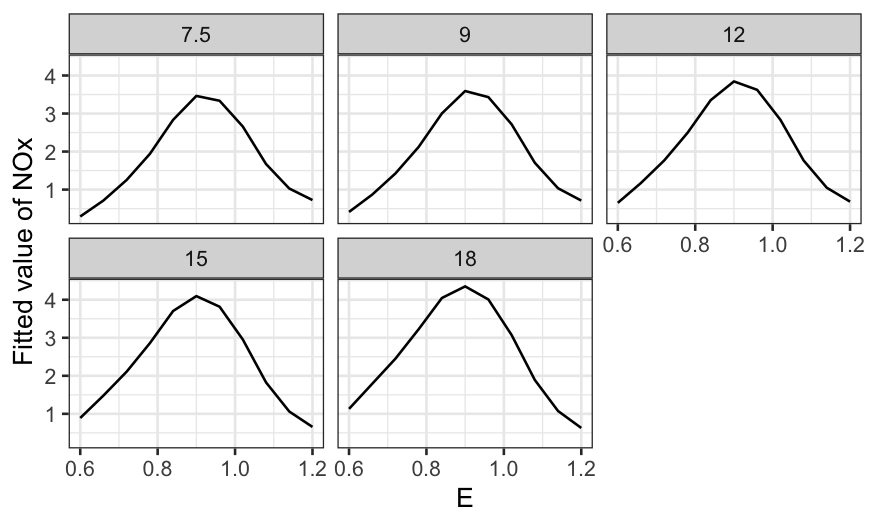
ggplot(coplot_ts, aes(x = hardness, y = abrasion.loss)) +
geom_point() +
facet_wrap(~ interval, ncol = 4) +
stat_smooth(method = "loess", method.args = list(span = .5, degree = 1), se = FALSE)## `geom_smooth()` using formula = 'y ~ x'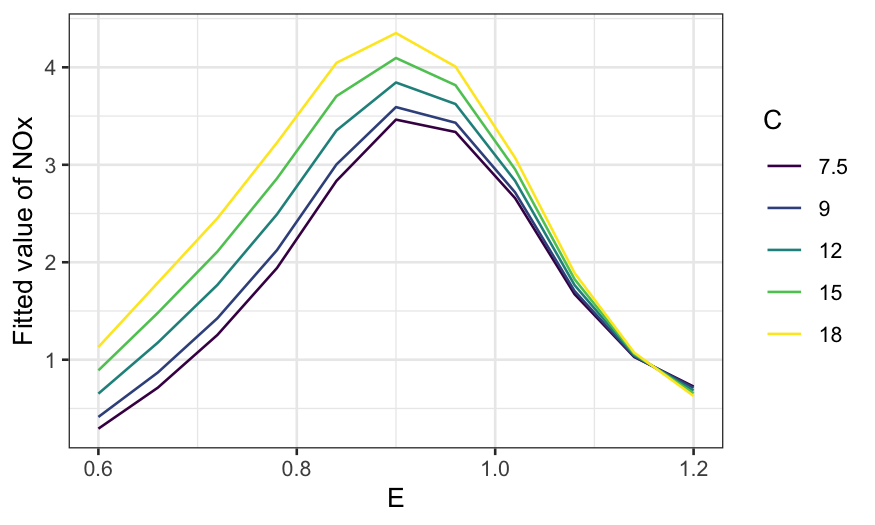
ggplot(coplot_ts, aes(x = hardness, y = abrasion.loss, color = interval)) +
stat_smooth(method = "loess", method.args = list(span = .5, degree = 1), se = FALSE)## `geom_smooth()` using formula = 'y ~ x'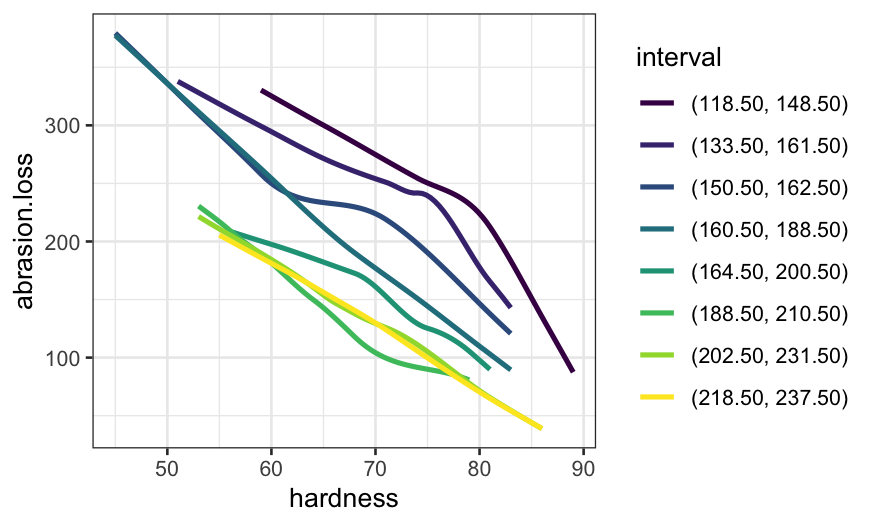
ggplot(coplot_ts, aes(x = hardness, y = abrasion.loss, color = interval)) +
stat_smooth(method = "lm", se = FALSE)## `geom_smooth()` using formula = 'y ~ x'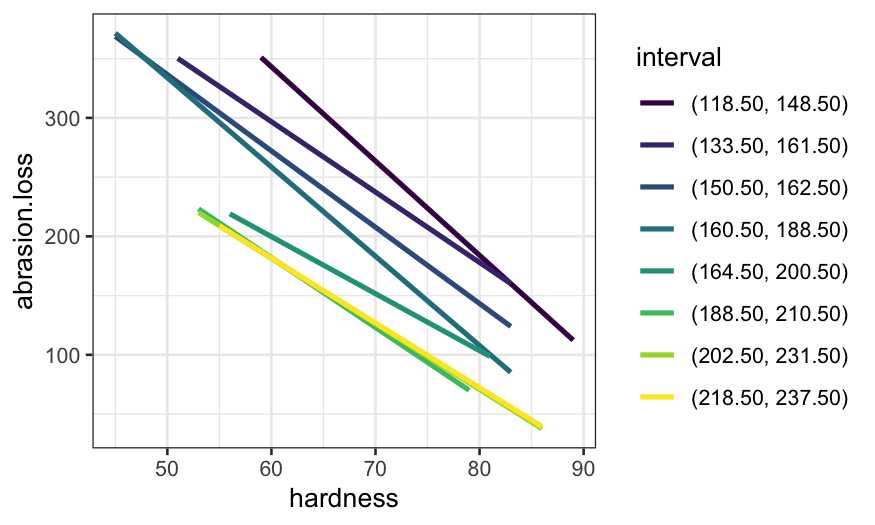
Let’s start off building a model with no interaction but with a
non-linear function of tensile.strength.
To do this, we need to:
tensile.strength.We want our non-linear function to be linear for values of
tensile.strength below 180, flat for values above 180, and
continuous. One such function is \[
f(x) = \begin{cases}
x - 180 & x \le 180\\
0 & x > 180
\end{cases}
\]
The way we would write this in R would be
tensile.strengthAnd to create a variable corresponding to this transformation of tensile strength, we could use
However, we don’t need to do that because Cleveland has already done
it for us (the variable ts.low already exists in the data
set and is exactly this function of tensile.strength).
To fit the model:
##
## Attaching package: 'MASS'## The following object is masked from 'package:dplyr':
##
## selectTo visualize the fitted model, we need to get fitted values from the model on a grid of values of the two predictors.
library(broom)
rubber.grid = expand.grid(hardness = c(54, 64, 74, 84),
tensile.strength = c(144, 162, 180, 198)) %>% data.frame
rubber.grid = rubber.grid %>% mutate(ts.low = tslow(tensile.strength))
rubber.predict = augment(rubber.rlm, newdata = rubber.grid)
rubber.predict## # A tibble: 16 × 4
## hardness tensile.strength ts.low .fitted
## <dbl> <dbl> <dbl> <dbl>
## 1 54 144 -36 357.
## 2 64 144 -36 289.
## 3 74 144 -36 222.
## 4 84 144 -36 154.
## 5 54 162 -18 298.
## 6 64 162 -18 230.
## 7 74 162 -18 162.
## 8 84 162 -18 94.8
## 9 54 180 0 238.
## 10 64 180 0 171.
## 11 74 180 0 103.
## 12 84 180 0 35.3
## 13 54 198 0 238.
## 14 64 198 0 171.
## 15 74 198 0 103.
## 16 84 198 0 35.3Once we have the fitted values, we can make a coplot of the fitted
model. We’ll start with hardness as the given variable:
ggplot(rubber.predict) +
geom_line(aes(x = tensile.strength, y = .fitted)) +
facet_grid(~ hardness) +
scale_y_continuous("Fitted abrasion loss") +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))
ggplot(rubber.predict) +
geom_line(aes(x = tensile.strength, y = .fitted, color = factor(hardness, ordered = TRUE))) +
guides(color = guide_legend(title = "Hardness")) +
scale_y_continuous("Fitted abrasion loss") +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))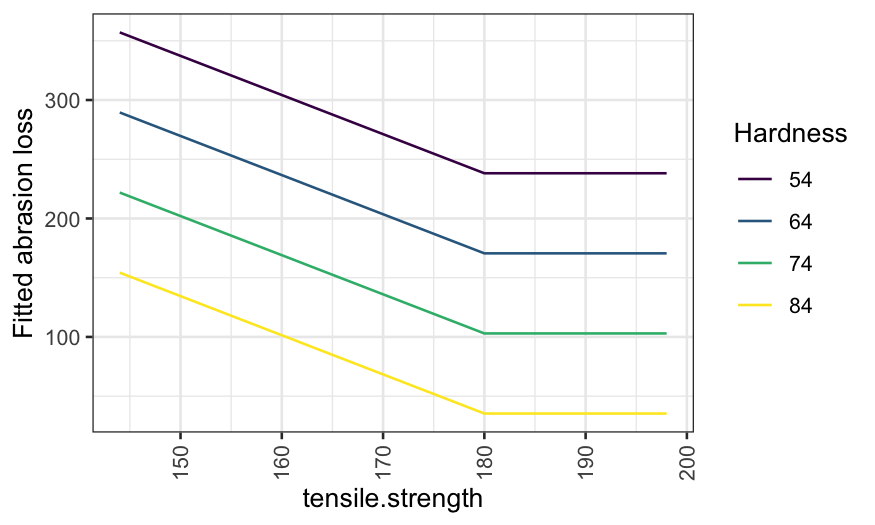
Note that the first plot is a coplot, the second doesn’t have a name but reports the same information in a different way.
Then a coplot with tensile.strength as the given
variable:
ggplot(rubber.predict) +
geom_line(aes(x = hardness, y = .fitted)) +
facet_grid(~ tensile.strength) +
scale_y_continuous("Fitted abrasion loss") +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))
ggplot(rubber.predict) +
geom_line(aes(x = hardness, y = .fitted, color = factor(tensile.strength, ordered = TRUE))) +
guides(color = guide_legend(title = "Tensile strength")) +
scale_y_continuous("Fitted abrasion loss") +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))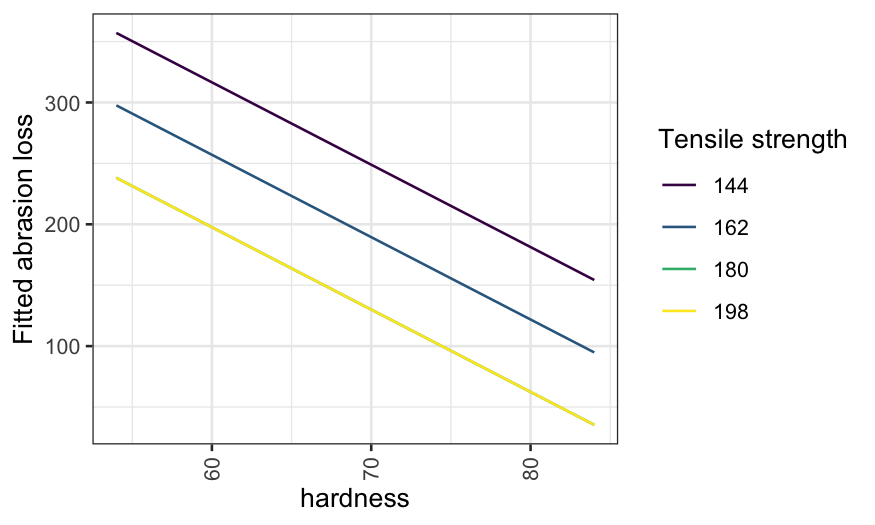
rubber.resid = data.frame(rubber, .resid = residuals(rubber.rlm))
ggplot(rubber.resid, aes(x = tensile.strength, y = .resid)) + geom_point() +
stat_smooth(method = "loess", span = 1, method.args = list(degree = 1, family = "symmetric")) +
geom_abline(slope = 0, intercept = 0) +
scale_y_continuous("Abrasion loss residuals")## `geom_smooth()` using formula = 'y ~ x'
ggplot(rubber.resid, aes(x = hardness, y = .resid)) + geom_point() +
stat_smooth(method = "loess", span = 1, method.args = list(degree = 1, family = "symmetric")) +
geom_abline(slope = 0, intercept = 0) +
scale_y_continuous("Abrasion loss residuals")## `geom_smooth()` using formula = 'y ~ x'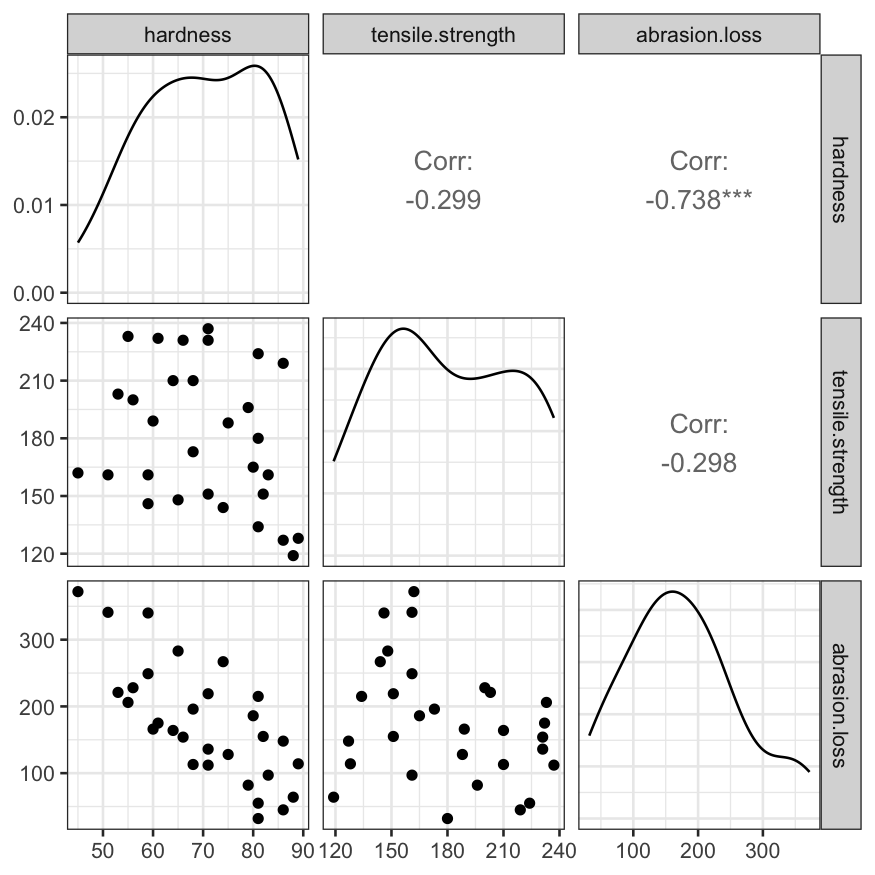
resid_co_hardness = make_coplot_df(rubber.resid, faceting_variable = "hardness", number_bins = 4)
ggplot(resid_co_hardness, aes(x = tensile.strength, y = .resid)) +
geom_point() +
facet_grid(~ interval) +
stat_smooth(method = "loess", method.args = list(degree = 1, family = "symmetric")) +
scale_y_continuous("Abrasion loss residuals")## `geom_smooth()` using formula = 'y ~ x'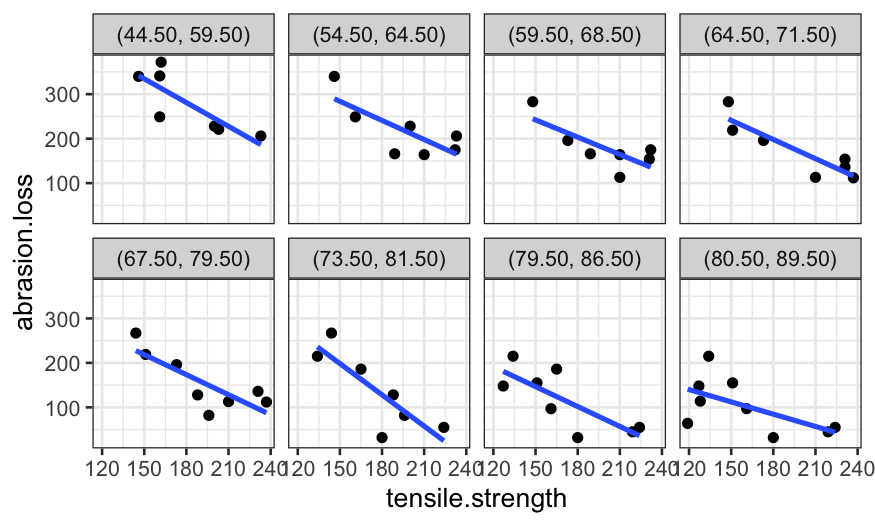
resid_co_ts = make_coplot_df(rubber.resid, faceting_variable = "tensile.strength", number_bins = 4)
ggplot(resid_co_ts, aes(x = hardness, y = .resid)) +
geom_point() +
facet_grid(~ interval) +
stat_smooth(method = "loess", method.args = list(degree = 1, family = "symmetric")) +
scale_y_continuous("Abrasion loss residuals")## `geom_smooth()` using formula = 'y ~ x'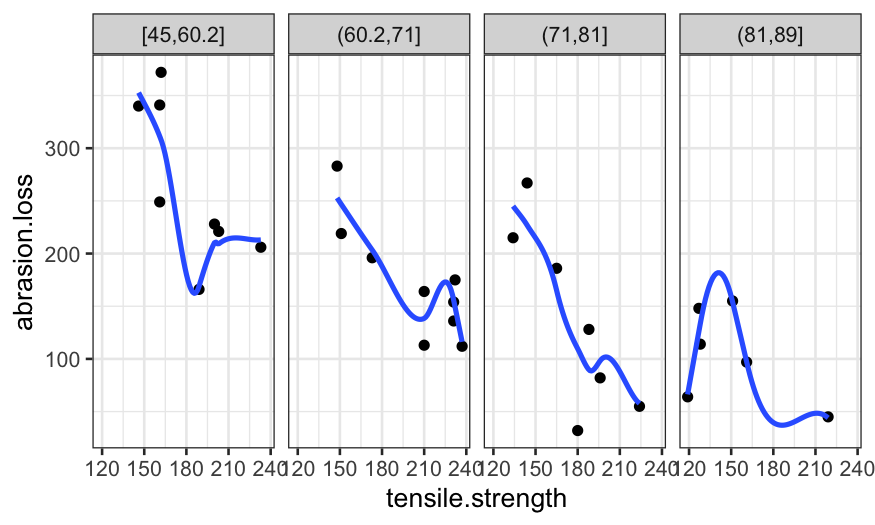
From the residual plots, it looks like we might actually do better
fitting an interaction between tensile.strength and
hardness.
Below, we fit a model with the interaction and make a coplot of the fitted and actual values.
We see that with the interaction, the slope of the fit below tensile strengh of 180 changes with hardness (steepest for the lowest values of hardness, shallowest for the highest hardnesses).
rubber.rlm = rlm(abrasion.loss ~ hardness * ts.low, data = rubber, psi = psi.bisquare)
coplot_hardness = coplot_hardness %>% mutate(interval_mean = get_interval_means(interval))
rubber.grid.final = expand.grid(hardness = unique(coplot_hardness$interval_mean),
tensile.strength = c(125, 180, 240)) %>% data.frame
rubber.grid.final = rubber.grid.final |> mutate(ts.low = tslow(tensile.strength))
rubber.predict.final = augment(rubber.rlm, newdata = rubber.grid.final)
rubber.predict.final = merge(rubber.predict.final,
unique(coplot_hardness[,c("interval", "interval_mean")]),
by.x = "hardness", by.y = "interval_mean")
ggplot(coplot_hardness, aes(x = tensile.strength, y = abrasion.loss)) +
geom_point() +
geom_line(aes(x = tensile.strength, y = .fitted), data = rubber.predict.final) +
facet_wrap(~ interval, ncol = 4) +
scale_y_continuous("Abrasion loss") +
scale_x_continuous("Tensile strength")