Generating random deviates

Agenda for today

Reading:

Random numbers vs pseudo-random numbers

True randomness: From nature

On computers: Everything deterministic, so we only have pseudo-random number generators

Linear congruential generator

A generator, so it makes a sequence of numbers.

Start off with \(X_0\).

Define \(X_{n+1} = (aX_n + c) \text{ mod } m\)

lcg_sequence <- function(a=5, c=12, m=16, seed = 10, n_deviates = 20) {
    sequence <- numeric(n_deviates)
    sequence[1] <- seed
    for(i in 2:n_deviates) {
        sequence[i] <- (a * sequence[i-1] + c) %% m
    }
  return(sequence)
}
lcg_sequence()
##  [1] 10 14  2  6 10 14  2  6 10 14  2  6 10 14  2  6 10 14  2  6
lcg_sequence(seed = 4)
##  [1]  4  0 12  8  4  0 12  8  4  0 12  8  4  0 12  8  4  0 12  8

Small values of \(m\), \(a\), \(c\) give sequences with relatively small period (time before the sequence repeats).

One recommendation:

random_unifs <- (lcg_sequence(a = 25214903917, c = 11, m = 2^48, seed = 2^47 - 17, n_deviates = 1000)) /
    2^48
head(round(random_unifs, digits = 3))
## [1] 0.500 0.498 0.715 0.444 0.353 0.458
mean(random_unifs <= .5)
## [1] 0.507
mean(random_unifs <= .8)
## [1] 0.804
mean(random_unifs <= .2)
## [1] 0.179

Problem setup

We have

We want

Inverse method

Let

\[ F^{[-1]}(y) = \text{inf}\{x : F(x) \ge y\}, \quad y \in [0,1] \]

If \(F\) is strictly increasing, we have \(F^{[-1]} = F^{-1}\).

Intuition:

Suppose \(F\) strictly increasing, \(F^{-1}\) exists, \(U \sim \text{Unif}(0,1)\).

Then \(F^{-1}(U) \sim F\).

Why?

\[ \begin{align*} P(F^{-1}(U) \le x) &= P(F(F^{-1}(U)) \le F(x)) \\ &= P(U \le F(x)) \\ &= F(x) \end{align*} \]

And so the CDF of \(F^{-1}(U)\) is \(F(x)\)

Inverse method: Procedure

Let \(F\) be the CDF of the target distribution, and let \[ F^{[-1]}(y) = \text{inf}\{x : F(x) \ge y\}, \quad y \in [0,1] \]

Inverse method: Exponential distribution

CDF for a random variable distributed exponential with rate 1:

\[ F(x) = 1 - e^{-x} \]

\[ F^{[-1]}(u) = -\log(1 - u) \]

\(F\) is strictly increasing and continuous, so just check that \(F(F^{-1}(u)) = u\).

Algorithm:

Note: We can also take \(X = -\log(U)\). Why?

Let’s check:

generate_exponential <- function() {
    U <- runif(1)
    X <- -log(1 - U)
    return(X)
}
random_exponentials <- replicate(n = 10000, generate_exponential())
grid <- seq(0,4, length.out = 200)
plot(sapply(grid, function(g) mean(random_exponentials <= g)) ~ grid, type = 'l',
     ylab = "Theoretical and Empirical CDF", xlab = "x")
points(pexp(grid) ~ grid, type = 'l', col = "red")

Inverse method: Discrete uniform distribution

We would like to sample uniformly from the set \(\{1,2,\ldots, n\}\)

CDF: \[ F(x) = \begin{cases} 0 & x < 0\\ \frac{\lfloor x \rfloor}{n} & x \in [0,n]\\ 1 & x > n \end{cases} \]

Inverse: \[ \begin{align*} F^{[-1]}(u) &= \text{inf} \{ x : F(x) \ge u\} \\ &= \begin{cases} -\infty & u = 0 \\ 1 & u \in (0, 1/n] \\ 2 & u \in (1/n, 2/n] \\ \vdots & \vdots \\ n & u \in ((n-1)/n, 1] \end{cases} \end{align*} \] Not including the points \(1/n, 2/n, \ldots, (n-1)/n\), this is equal to \(\lfloor nu \rfloor + 1\).

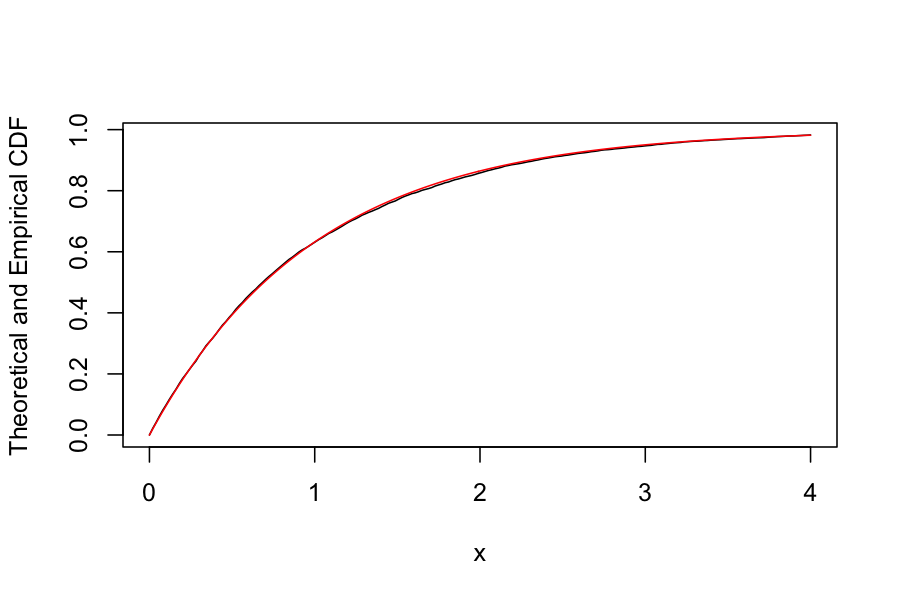
Let’s check:

generate_discrete_uniform <- function(n) {
    U <- runif(1)
    return(floor(n * U) + 1)
}
discrete_uniforms <- replicate(n = 10000, generate_discrete_uniform(3))
head(discrete_uniforms)
## [1] 1 3 3 1 1 1
table(discrete_uniforms) / length(discrete_uniforms)
## discrete_uniforms
##      1      2      3 
## 0.3330 0.3332 0.3338

Acceptance-Rejection Method

Problem setup:

Acceptance-Rejection Procedure

  1. Sample \(U \sim \text{Uniform}[0,1]\) and \(Z \sim g\)

  2. If \(U \le \frac{f(Z)}{ c g(Z)}\), return \(Z\)

  3. Otherwise, return to 1

Acceptance-Rejection Method: Why does it work?

Probability of generating an accepted value in \((x, x + dx)\) is proportional to \[ g(x) dx \frac{f(x)}{h(x)} = \frac{1}{c} f(x) dx \]

Notes

Acceptance-Rejection Method: Example

We want \(X\) with density \[ f_X(x) = \frac{2}{\sqrt{2\pi}} e^{-x^2 / 2}, \quad x \ge 0 \]

Let \(g(x) = e^{-x}\), \(x \ge 0\) (exponential with rate 1)

Let \(c = \sqrt {2e / \pi} \approx 1.32\) (obtained by finding the maximum of \(f_X(x) / g(x)\))

Check: \(f_X(x) \le cg(x)\) for all \(x \ge 0\)

fX <- function(x) 2 / sqrt(2 * pi) * exp(-x^2 / 2)
g <- function(x) exp(-x)
c <- sqrt(2 * exp(1) / pi)
grid <- seq(0, 4, length.out = 200)
plot(fX(grid) ~ grid, type = 'l', ylim = c(0, 1.5))
points(c * g(grid) ~ grid, type = 'l', col = 'red')

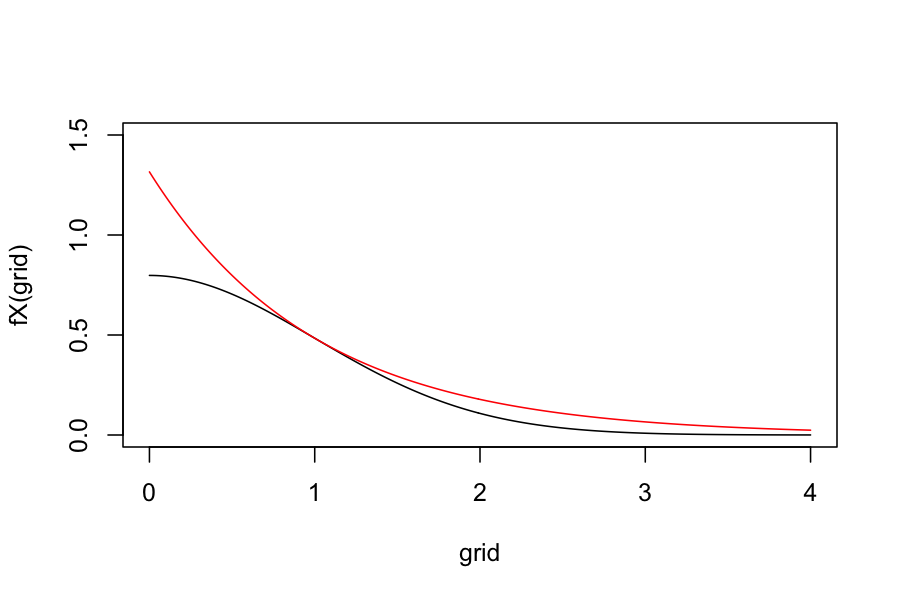
Overall algorithm:

  1. Generate \(Z \sim \text{Exp}(1)\)

  2. Generate \(U \sim \text{Unif}(0,1)\)

  3. If \(U \le \frac{f_X(Z)}{ c g(Z)} = \frac{2}{\sqrt{e}}\exp(-Z^2 / 2 + Z)\), return \(Z\)

Let’s check:

gen_half_normal <- function() {
    fX <- function(x) 2 / sqrt(2 * pi) * exp(-x^2 / 2)
    g <- function(x) exp(-x)
    c <- sqrt(2 * exp(1) / pi)
    while(TRUE) {
        U <- runif(1)
        Z <- rexp(1, rate = 1)
        if(U <= fX(Z) / (c * g(Z))) {
            return(Z)
        }
    }
}
half_normals <- replicate(n = 10000, gen_half_normal())
signs <- ifelse(runif(10000) >= .5, -1, 1)
normals <- half_normals * signs
qqnorm(normals)

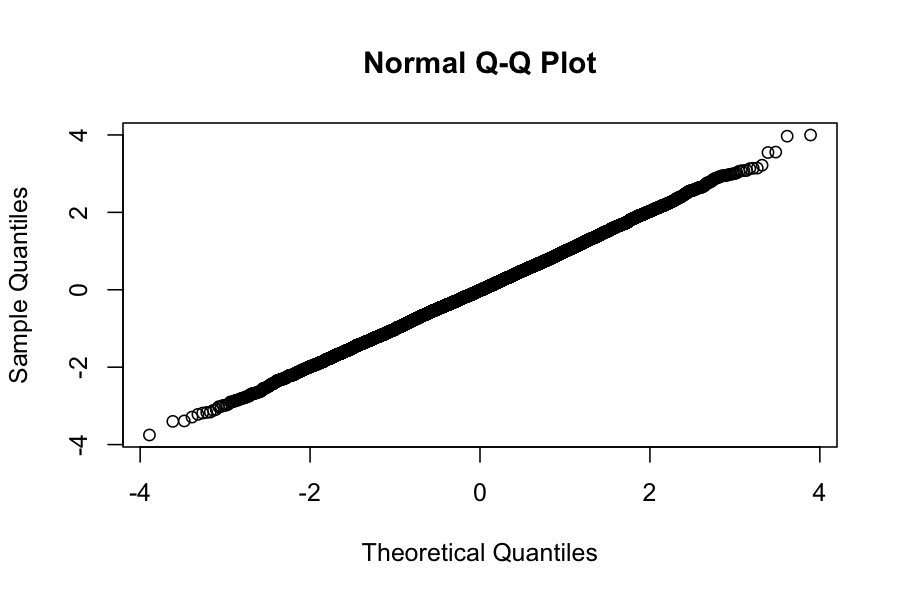
Why might we want to do this?

Summing up