More optimization…
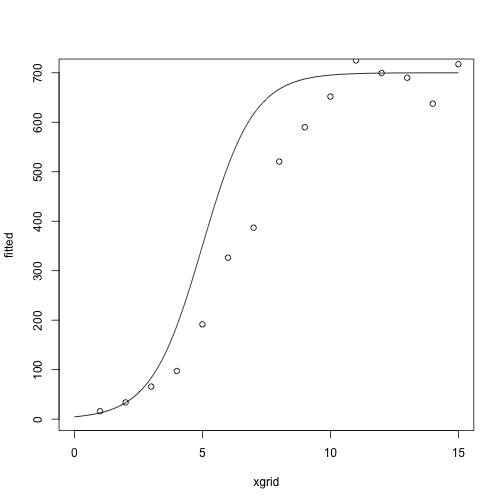
Today: modifications of Newton’s method
- Fisher scoring (if you want to make sure the Hessian term is
negative definite)
- Hessian approximations (if it takes too long to re-compute/re-invert
the Hessian)
- Gradient descent (if you don’t want to ever compute or invert the
Hessian)
Reading:
- Lange Chapter 11.1-11.4, 11.6
Fisher Scoring
Idea: Use the expected information, \(I(\theta)= E[-d^2 \ell(\theta)]\) instead
of the observed information, \(d^2
\ell(\theta)\).
Algorithm:
- Pick a starting parameter estimate \(\theta_0\)
- Set \(\theta_{n+1} = \theta_n +
I(\theta)^{-1} d\ell(\theta_n)\)
\(I(\theta)\) often coincides with
\(-d^2 \ell(\theta)\), in which case
Fisher Scoring is exactly the same as Newton’s method.
Sometimes \(I(\theta)\) is easier to
compute than \(-d^2 \ell(\theta)\).
Example: Non-linear least squares
Inputs:
- Data \(y_1,\ldots, y_n\).
- Covariates \(x_1,\ldots,
x_n\).
- Parameter vector \(\theta\)
- Non-linear function \(\mu\), with
\(\mu(x, \theta_1, \theta_2, \theta_3) =
\frac{\theta_3}{1 + e^{-\theta_1 - \theta_2 x}}\)
- For notational purposes, let \(\mu_i
(\theta) = \mu(x_i, \theta_1,\theta_2,\theta_3)\).
Model: \[
y_i \sim N(\mu_i(\theta), \sigma^2)
\]
Log likelihood: \[
\ell(\theta) = - \frac{1}{2} \sum_{i=1}^n (y_i - \mu_i(\theta))^2 + C
\]
Gradient/score: \[
\begin{align*}
d\ell(\theta) &= \sum_{i=1}^n (y_i - \mu_i(\theta)) d\mu_i(\theta)\\
d\mu_i(\theta) &= \begin{pmatrix}
\frac{\theta_3 e^{-\theta_1 - \theta_2 x}}{(1 + e^{-\theta_1 - \theta_2
x})^2} \\
\frac{x\theta_3 e^{-\theta_1 - \theta_2 x}}{(1 + e^{-\theta_1 - \theta_2
x})^2} \\
\frac{1}{(1 + e^{-\theta_1 - \theta_2 x})^2}
\end{pmatrix}
\end{align*}
\]
Hessian: \[
d^2 \ell(\theta) = -\sum_{i=1}^n d \mu_i(\theta) d \mu_i(\theta)^T +
\sum_{i=1}^n (y_i - \mu_i(\theta))d^2 \mu_i(\theta)
\]
Information: \[
I(\theta) = E[-d^2 \ell(\theta)] = \sum_{i=1}^n d\mu_i(\theta)
d\mu_i(\theta)^T
\]
Example
fisher_scoring_iterate = function(x, y, theta_current) {
score = compute_score(x, y, theta_current)
information = compute_information(x, theta_current)
theta_new = theta_current + solve(information) %*% score
}
compute_score = function(x, y, theta) {
fitted = nonlin_function(x, theta)
grad_mu = compute_grad_mu(x, theta)
rowSums(sweep(grad_mu, 2, STATS = y - fitted, FUN = "*"))
}
compute_information = function(x, theta) {
## a 3 x n matrix
grad_mu = compute_grad_mu(x, theta)
grad_mu %*% t(grad_mu)
}
compute_grad_mu = function(x, theta) {
denom = 1 + exp(-theta[1] - theta[2] * x)
g1 = theta[3] * exp(-theta[1] - theta[2] * x) / denom^2
g2 = x * theta[3] * exp(-theta[1] - theta[2] * x) / denom^2
g3 = 1 / denom
return(rbind(g1, g2, g3))
}
nonlin_function = function(x, theta) {
theta[3] / (1 + exp(-theta[1] - theta[2] * x))
}
At the starting values:
library(NISTnls)
data(Ratkowsky3)
x = Ratkowsky3$x
y = Ratkowsky3$y
theta = c(-5, 1, 700)
xgrid = seq(0, 15, length.out = 1000)
fitted = nonlin_function(xgrid, theta)
plot(fitted ~ xgrid, type = 'l')
points(y ~ x)
After one iteration:
(theta = fisher_scoring_iterate(x, y, theta))
## [,1]
## g1 -3.3298463
## g2 0.4649027
## g3 677.8340519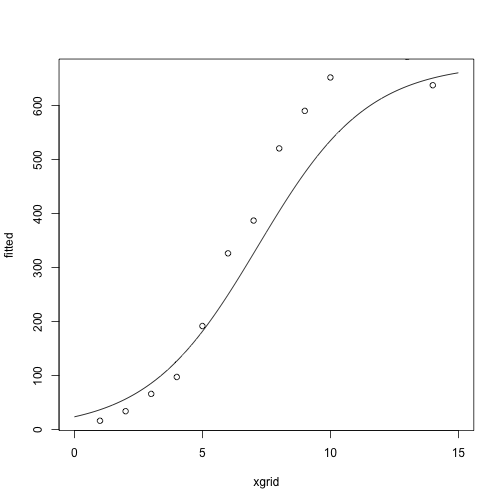
fitted = nonlin_function(xgrid, theta)
plot(fitted ~ xgrid, type = 'l')
points(y ~ x)
After two iterations:
(theta = fisher_scoring_iterate(x, y, theta))
## [,1]
## g1 -4.2780124
## g2 0.6775608
## g3 664.2494602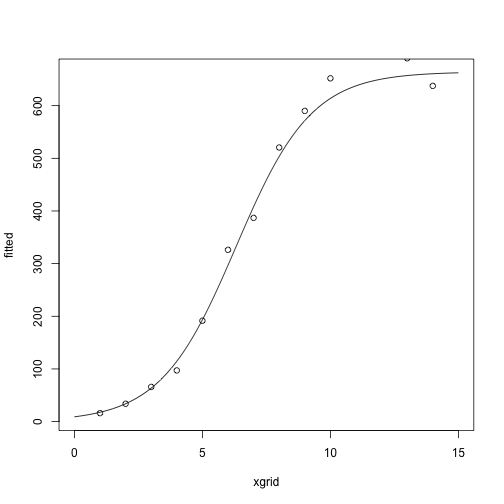
fitted = nonlin_function(xgrid, theta)
plot(fitted ~ xgrid, type = 'l')
points(y ~ x)
After several more iterations
for(i in 1:5) {
theta = fisher_scoring_iterate(x, y, theta)
print(theta)
}
## [,1]
## g1 -4.438590
## g2 0.687286
## g3 702.939738
## [,1]
## g1 -4.4435690
## g2 0.6887401
## g3 702.8457366
## [,1]
## g1 -4.4424684
## g2 0.6885486
## g3 702.8741477
## [,1]
## g1 -4.4425736
## g2 0.6885677
## g3 702.8711538
## [,1]
## g1 -4.4425628
## g2 0.6885657
## g3 702.8714589
fitted = nonlin_function(xgrid, theta)
plot(fitted ~ xgrid, type = 'l')
points(y ~ x)
Compare with
nls(y ~ b3 / ((1+exp(-b1-b2*x))), data = Ratkowsky3,
start = c(b1 = -5, b2 = 0.75, b3 = 700),
trace = TRUE)
## 12935.59 (6.67e-01): par = (-5 0.75 700)
## 8971.367 (7.04e-02): par = (-4.363867 0.6765795 703.9695)
## 8930.131 (5.51e-03): par = (-4.447056 0.6894499 702.678)
## 8929.885 (5.50e-04): par = (-4.442017 0.6884684 702.8859)
## 8929.883 (5.62e-05): par = (-4.442618 0.6885758 702.8699)
## 8929.883 (5.78e-06): par = (-4.442558 0.6885649 702.8716)
## Nonlinear regression model
## model: y ~ b3/((1 + exp(-b1 - b2 * x)))
## data: Ratkowsky3
## b1 b2 b3
## -4.4426 0.6886 702.8716
## residual sum-of-squares: 8930
##
## Number of iterations to convergence: 5
## Achieved convergence tolerance: 5.777e-06
Quasi-Newton Methods
Idea: If you don’t move very far in one step, the Hessian shouldn’t
change that much either.
Instead of recomputing the Hessian at each step, compute an
approximate update.
- Start with an initial guess at a parameter \(\theta^{(0)}\).
- Let \(A^{(0)} = d^2
\ell(\theta)\).
- Set \(\theta^{(n+1)} = \theta^{(n)} -
(A^{(n)})^{-1} d \ell(\theta^{(n)})\)
- Set \(A^{(n+1)} = A^{(n)} - c^{(n)}
v^{(n)} (v^{(n)})^T\)
\(A^{(n)}\) are approximations to
the Hessian.
Idea behind Hessian update: Taylor series again:
\[
d\ell(\theta^{(n)}) \approx d\ell(\theta^{(n+1)}) + d^2
\ell(\theta^{(n+1)})(\theta^{(n)} - \theta^{(n+1)})
\]
Rearranging: \[
d\ell(\theta^{(n)}) - d\ell(\theta^{(n+1)})\approx d^2
\ell(\theta^{(n+1)})(\theta^{(n)} - \theta^{(n+1)})
\]
Finding an approximation \(A^{(n+1)}\) of \(-d^2\ell(\theta^{(n+1)})\) that satisfies
the equation above is called the secant condition.
Several different ways to make the approximation:
- Symmetric rank-1 update is Davidon’s method, described in
Lange.
- Symmetric rank-2 update is BFGS
(Broyden–Fletcher–Goldfarb–Shanno).
For notation, let \[
\begin{align*}
g^{(n)} &= d\ell(\theta^{(n)}) - d \ell(\theta^{(n+1)}) \\
s^{(n)} &= \theta^{(n)} - \theta^{(n+1)}
\end{align*}
\]
We can rewrite the secant condition \[
d\ell(\theta^{(n)}) - d\ell(\theta^{(n+1)})\approx d^2
\ell(\theta^{(n+1)})(\theta^{(n)} - \theta^{(n+1)})
\] as \[
-A^{(n+1)} s^{(n)} = g^{(n)}
\]
Davidon’s method is a symmetric rank-1 update.
\[
A^{(n+1)} = A^{(n)} - c^{(n)} v^{(n)} (v^{(n)})^T
\]
where \[
c^{(n)} = \frac{1}{(g^{(n)} + A^{(n)} s^{(n)})^T s^{(n)}}
\]
\[
v^{(n)} = g^{(n)} + A^{(n)} s^{(n)}
\]
(verify on your own that this satisfies the secant condition)
BFGS is a symmetric rank-2 update.
\[
A^{(n+1)} = A^{(n)} + \alpha u u^T + \beta v v^T
\]
\(u = y^{(k)}\), \(v = A^{(n)} s^{(n)}\), \(\alpha = -1 / (g^{(k)})^T s^{(k)}\), \(\beta = - 1 / (s^{(k)})^T B^{(k)}
s^{(k)}\)
Why are these useful?
- This makes it easy to compute an approximation of \(-d^2 \ell(\theta)\), but we still need to
invert it to take an approximate Newton step
\[
(A + UCV)^{-1}= A^{-1} - A^{-1} U(C^{-1} + VA^{-1} U)^{-1} V A^{-1}
\]
Gradient descent
Our problem:
\[
\text{minimize}_x \quad f(x)
\]
Note that we’re doing minimization instead of maximization now so
that the notation matches the reading, but any minimization problem can
be recast as a maximization and vice versa.
Descent Methods
General algorithm:
Start with a point \(x\)
Repeat
- Choose a descent direction \(\Delta
x\)
- Update: \(x \leftarrow x + t \Delta
x\)
Until the stopping criterion is satisfied, usually \(\|\nabla f(x)\|_2 \le \epsilon\).
Gradient descent
In gradient descent, we take \(\Delta x = -
\nabla f(x)\).
Overall algorithm:
Start with a point \(x\)
Repeat
- \(\Delta x \leftarrow - \nabla
f(x)\).
- Choose a step size t. Can be deterministic based on the step or
adaptive.
- Update: \(x \leftarrow x + t \Delta
x\)
Until the stopping criterion is satisfied, usually \(\|\nabla f(x)\|_2 \le \epsilon\).
Choosing the step size
A lot of options, grouped into deterministic and adaptive.
Deterministic methods:
- Time-based schedules, e.g. \(t_{n+1} = t_n
/ (1 + di)\) (\(d\) a decay
parameter, \(i\) the iteration)
- Step-based schedules, e.g. \(t_n = t_0 /
(1 + i / \tau)\) (\(\tau\) a
“search time” parameter, \(i\) the
iteration, \(t_0\) an initial step
size).
- Exponential schedules, e.g. \(t_n = t_0
e^{-di}\) (\(i\) the iteration,
\(d\) a decay parameter, \(t_0\) an initial step size).
Adaptive methods:
Gradient descent example in pictures
Iterates of gradient descent with backtracking line search, for
minimizing \(f(x_1, x_2) = \exp(x_1 + 3 x_2 -
.1) + \exp(x_1 - 3 x_2 - .1) + \exp(-x_1 - .1)\)
Contours represent the boundaries of the sublevel sets of
the function: \(\{x : f(x) \le
a\}\).
Gradient descent example for normal mean
Suppose \(x_1, \ldots, x_n \sim N(\theta,
1)\).
We want to know \(\theta\), and we
will get \(\hat \theta\) by minimizing
the negative log likelihood: \[
-\ell(\theta) = C + \frac{1}{2} \sum_{i=1}^n (x_i - \theta)^2
\]
A descent direction for the negative log likelihood is the negative
derivative of the negative log likelihood: \[
-d(-\ell(\theta)) = \sum_{i=1}^n (x_i - \theta)
\]
Functions for the log likelihood:
neg_log_lik = function(theta, x) {
return(.5 * sum((x - theta)^2))
}
neg_deriv = function(theta, x) {
return(sum(x - theta))
}
step_size = function(i, eta0, tau) {
return(eta0 / (1 + i / tau))
}
step_size_exponential = function(i, t0, d) {
return(t0 * exp(-i * d))
}
set.seed(0)
x = rnorm(n = 20, mean = 5, sd = 1)
mean(x)
## [1] 4.998221
theta = 0
niter = 1000
intermediate_theta_vals = numeric(niter)
for(i in 1:niter) {
theta = theta + step_size(i, eta0 = 1, tau = 40) * neg_deriv(theta, x)
intermediate_theta_vals[i] = theta
#cat(sprintf("Value of theta at iteration %i: %.2f\n", i, theta))
}
theta
## [1] 4.998221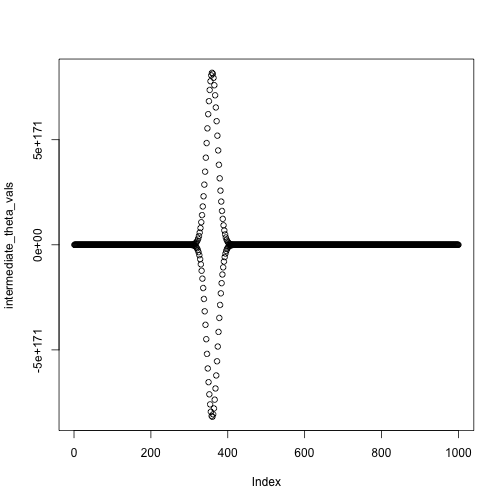
plot(intermediate_theta_vals)
Logistic regression
Set up the data the same way as last time:
set.seed(1)
theta_true = c(1,2)
n = 100
X = cbind(rep(1, n), rnorm(n, mean = 0, sd = 1))
colnames(X) = c("Intercept", "x")
p = exp(X %*% theta_true) / (1 + exp(X %*% theta_true))
y = rbinom(n = n, size = 1, prob = p)
plot(y ~ X[,"x"])
points(p ~ X[,"x"], col = "red")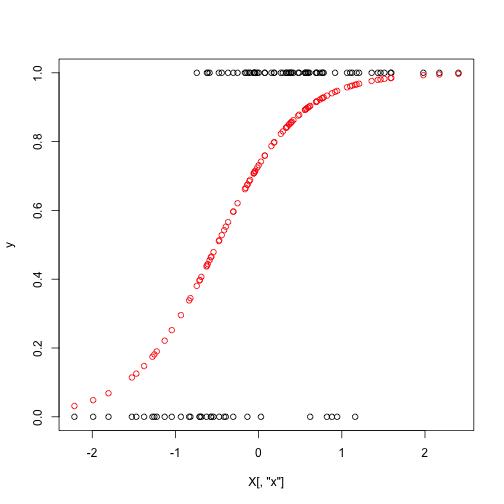
Set up the gradient function (minimizing the negative log likelihood,
need the negative gradient of the negative log likelihood or the
gradient of the log likelihood):
neg_gradient = function(theta, X, y) {
p = exp(X %*% theta) / (1 + exp(X %*% theta))
return(t(X) %*% (y - p))
}
Do our gradient calculations:
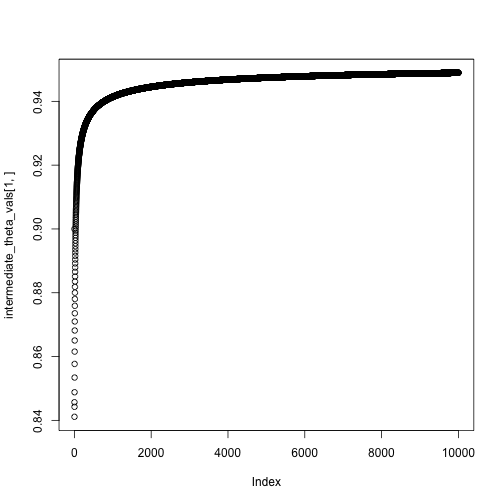
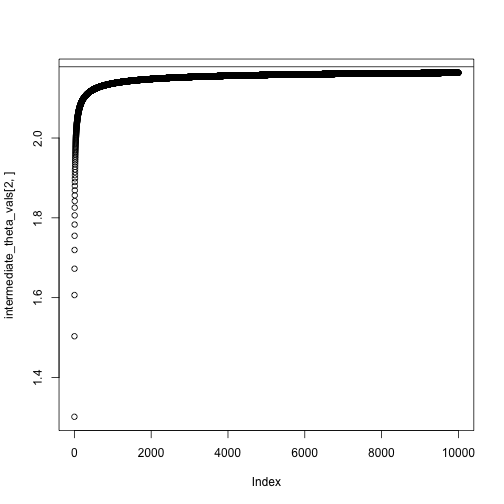
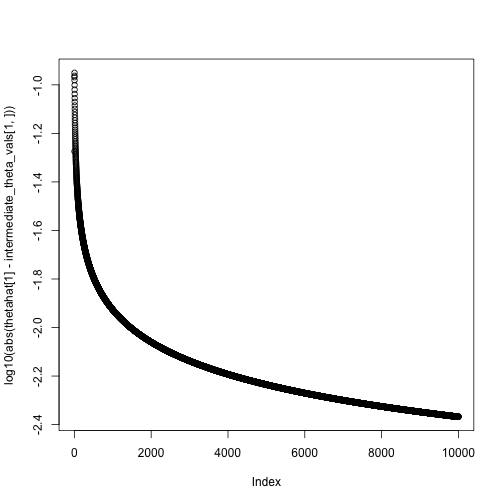
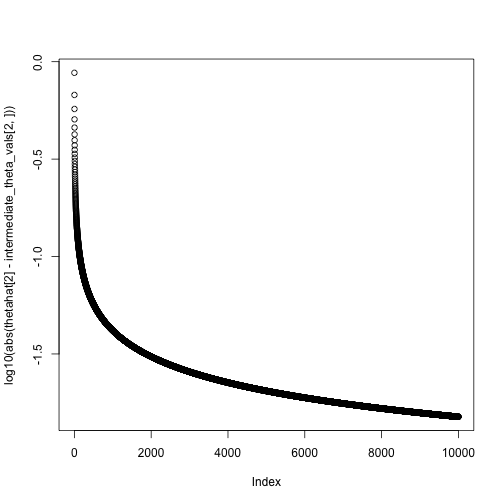
theta = c(0,0)
niter = 10000
intermediate_theta_vals = matrix(0, nrow = 2, ncol = niter)
for(i in 1:niter) {
theta = theta + step_size(i, eta0 = .1, tau = 1) * neg_gradient(theta, X, y)
intermediate_theta_vals[,i] = theta
#cat(sprintf("Value of theta at iteration %i: %.2f\n", i, theta))
}
theta
## [,1]
## Intercept 0.9489461
## x 2.1634107
(thetahat = coef(glm(y ~ 0 + X, family = "binomial")))
## XIntercept Xx
## 0.9532323 2.1784561
plot(intermediate_theta_vals[1,])
abline(h = thetahat[1])
plot(intermediate_theta_vals[2,])
abline(h = thetahat[2])
plot(log10(abs(thetahat[1] - intermediate_theta_vals[1,])))
plot(log10(abs(thetahat[2] - intermediate_theta_vals[2,])))
Summing up
- Everything we’ve seen has an interpretation as Newton’s method with
some approximation of the Hessian standing in for the real thing
- You need to trade off between using the analytic information you
have about the problem and computational complexity.