## The proposal distribution is normal, centered at the current state, standard deviation .3
proposal_function = function(x) rnorm(n = 1, mean = x, sd = .3)
## The target distribution is N(0,1)
target_distribution = function(x) .25 * dnorm(x, mean = 1, sd = 1) + .75 * dnorm(x, mean = 5, sd = .2)
n_samples = 1000
chain_output = numeric(n_samples)
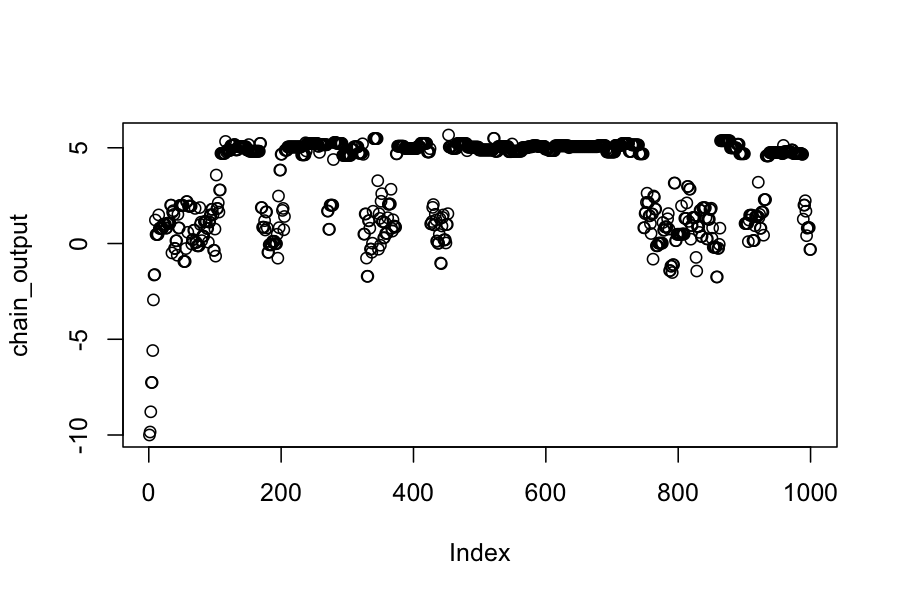
chain_output[1] = -10
for(i in 2:n_samples) {
chain_output[i] = sample_with_symmetric_proposal(proposal_function, target_distribution, chain_output[i-1])
}
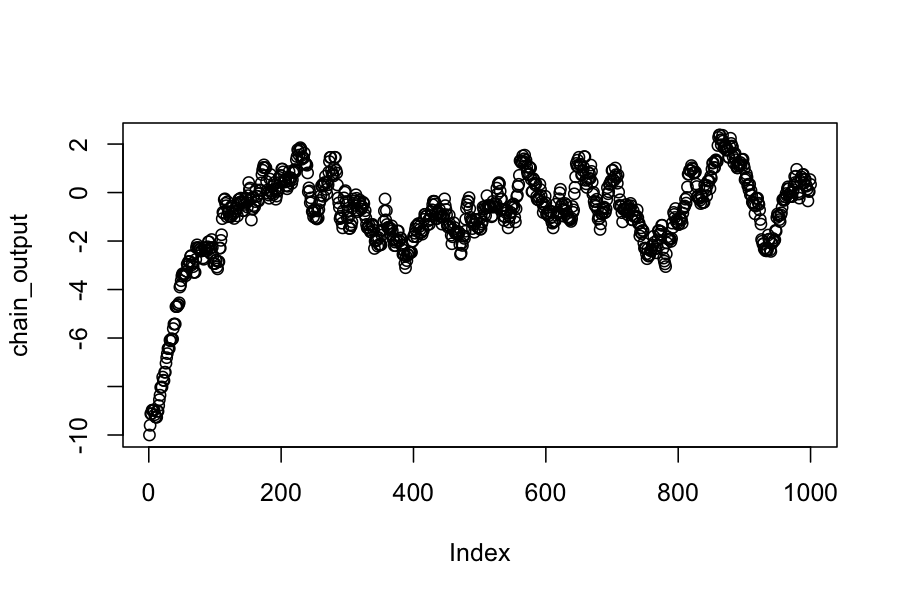
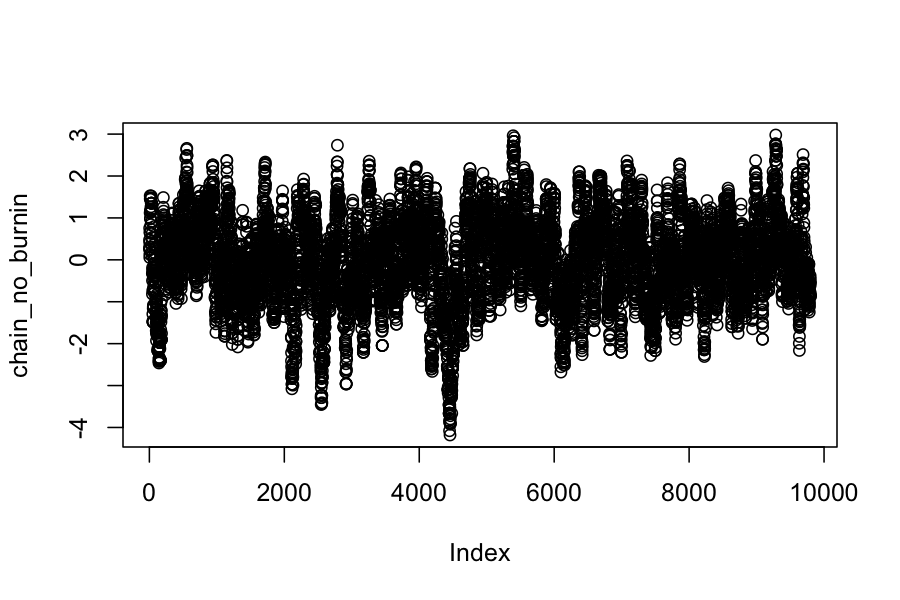
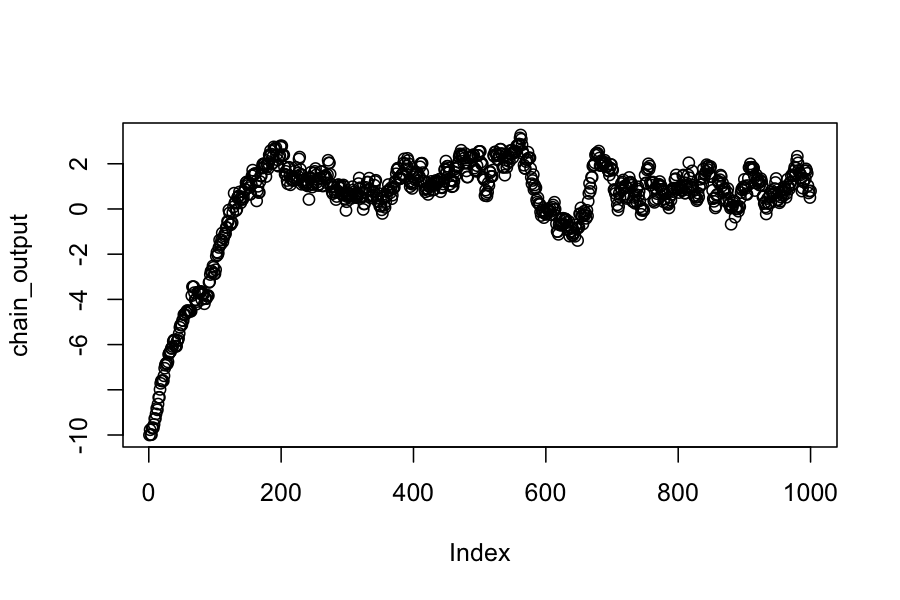
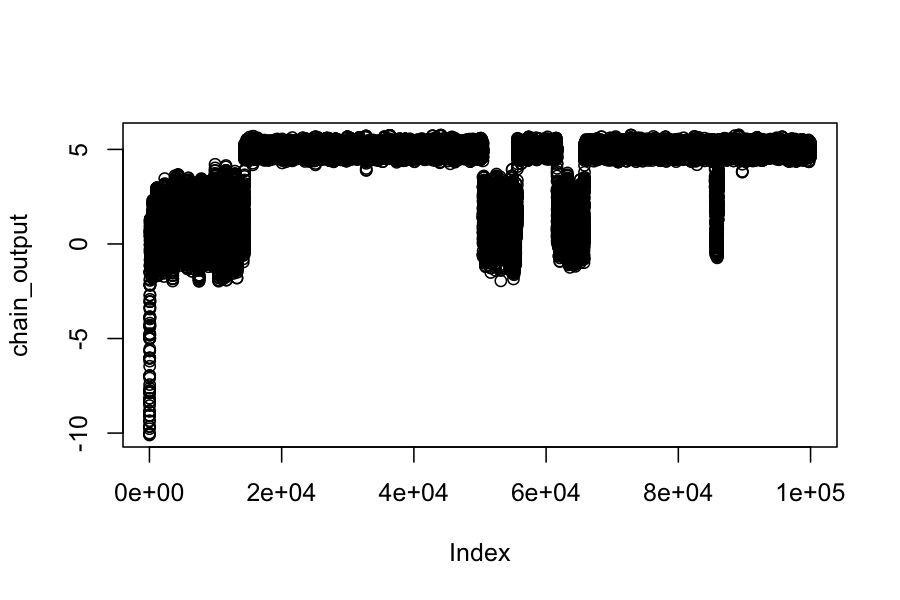
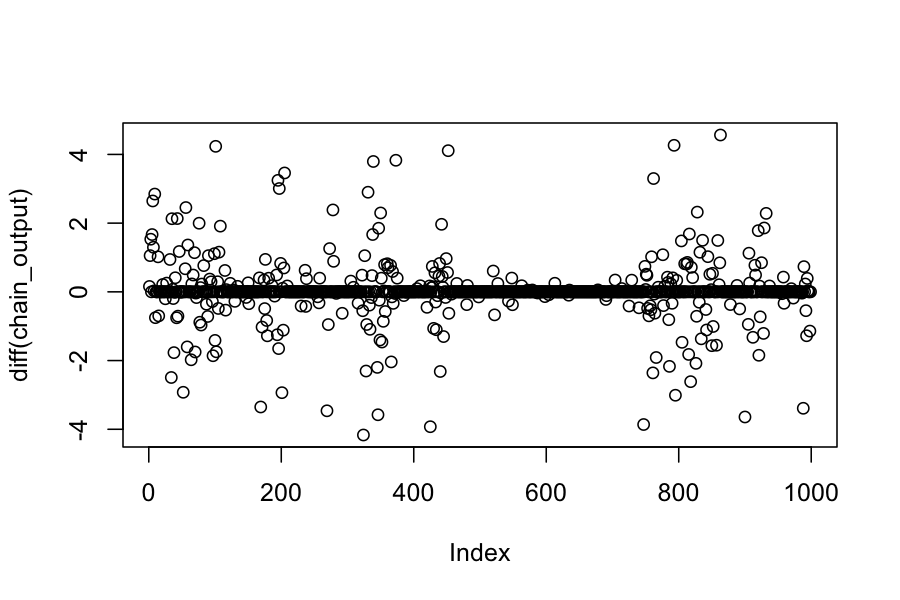
plot(chain_output)